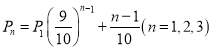题目内容

【题目】已知双曲线的左、右焦点分别、，过的直线交双曲线右支于，两点.的平分线交于，若，则双曲线的离心率为( )

A.B.2C.D.

【答案】A

【解析】

首先取中点，连接，，利用平面向量加法的几何意义得到轴，，再根据勾股定理列出等式，计算离心率即可.

取中点，连接，，如图所示：

[Failed to download image : http://192.168.0.10:8086/QBM/2020/6/18/2487522753945600/2488179565289472/EXPLANATION/0643573483c14d6289b6f64992bd8c2c.png]

由，可知四边形为平行四边形.

又∵为的平分线，∴四边形为菱形.

∵，∴为中点，

∵，∴为中点，

由双曲线的对称性可知：轴，点在轴上.

∴，

由双曲线定义得：，

所以，

∴，即，

整理得，所以.

故选：A

练习册系列答案
相关题目

【题目】如图，在四棱锥P-ABCD中，底面ABCD为矩形，平面PCD⊥平面ABCD，AB=2，BC=1，，E为PB中点．

（Ⅰ）求证：PD∥平面ACE；

（Ⅱ）求证：PD⊥平面PBC；

（Ⅲ）求三棱锥E-ABC的体积．

【题目】已知椭圆的离心率为，过定点的直线l与椭圆E相交于A，B两点，C为椭圆的左顶点，当直线l过点时，（O为坐标原点）的面积为．

（1）求椭圆E的方程；

（2）求证：当直线l不过C点时，为定值．

【题目】函数f（x）＝Asin（ωx+φ）+B的部分图象如图所示，其中A＞0，ω＞0，|φ|．

（Ⅰ）求函数y＝f（x）解析式；

（Ⅱ）求x∈[0，]时，函数y＝f（x）的值域．

【题目】如图，在三棱锥D-ABC中为锐角三角形，平面ACD⊥平面.

（1）求证：CD⊥平面ABC

（2）若直线BD与平面ACD所成角的正弦值为，求二面角D-AB-C的余弦值.

【题目】已知抛物线：的焦点为，过作斜率为的直线交于，两点，以线段为直径的圆.当时，圆的半径为2.

（1）求的方程；

（2）已知点，对任意的斜率，圆上是否总存在点满足，请说明理由.

【题目】在“挑战不可能”的电视节目上，甲、乙、丙三个人组成的解密团队参加一项解密挑战活动，规则是由密码专家给出题目，然后由个人依次出场解密，每人限定时间是分钟内，否则派下一个人.个人中只要有一人解密正确，则认为该团队挑战成功，否则挑战失败.根据甲以往解密测试情况，抽取了甲次的测试记录，绘制了如下的频率分布直方图.

（1）若甲解密成功所需时间的中位数为，求、的值，并求出甲在分钟内解密成功的频率；

（2）在“挑战不可能”节目上由于来自各方及自身的心理压力，甲，乙，丙解密成功的概率分别为，其中表示第个出场选手解密成功的概率，并且定义为甲抽样中解密成功的频率代替，各人是否解密成功相互独立.

①求该团队挑战成功的概率；

②该团队以从小到大的顺序按排甲、乙、丙三个人上场解密，求团队挑战成功所需派出的人员数目的分布列与数学期望.

【题目】某病毒研究所为了研究温度对某种病毒的影响，在温度t（℃）逐渐升高时，连续测20次病毒的活性指标值y，实验数据处理后得到下面的散点图，将第1～14组数据定为A组，第15～20组数据定为B组．

（Ⅰ）某研究员准备直接根据全部20组数据用线性回归模型拟合y与t的关系，你认为是否合理？请从统计学的角度简要说明理由．

（Ⅱ）若根据A组数据得到回归模型，根据B组数据得到回归模型，以活性指标值大于5为标准，估计这种病毒适宜生存的温度范围（结果精确到0.1）．

（Ⅲ）根据实验数据计算可得：A组中活性指标值的平均数，方差；B组中活性指标值的平均数，方差．请根据以上数据计算全部20组活性指标值的平均数和方差．

【题目】已知曲线上的点到的距离比它到直线的距离少3.

（1）求曲线的方程；

（2）过点且斜率为的直线交曲线于，两点，交圆于，两点，，在轴上方，过点，分别作曲线的切线，，，求与的面积的积的取值范围.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网