题目内容
5.由计算机产生2n个0~1之间的均匀随机数x1,x2,…xn,y1,y2,…yn,构成n个数对(x1,y1),(x2y2),…(xn,yn)其中两数能与1构成钝角三角形三边的数对共有m个,则用随机模拟的方法得到的圆周率π的近似值为$\frac{4m}{n}+2$.分析 利用n对0~1之间的均匀随机数x,y,满足$\left\{\begin{array}{l}0<x<1\\ 0<y<1\end{array}\right.$,相应平面区域面积为1,两个数能与1构成钝角三角形三边的数对(x,y),满足$\left\{\begin{array}{l}{x^2}+{y^2}<1\\ x+y>1\end{array}\right.$且$\left\{\begin{array}{l}0<x<1\\ 0<y<1\end{array}\right.$,面积为$\frac{π}{4}-\frac{1}{2}$,结合面积比,即可得出结论.
解答 解:由题意,n对0~1之间的均匀随机数x,y,满足$\left\{\begin{array}{l}0<x<1\\ 0<y<1\end{array}\right.$,相应平面区域面积为1,两个数能与1构成钝角三角形三边的数对(x,y),满足$\left\{\begin{array}{l}{x^2}+{y^2}<1\\ x+y>1\end{array}\right.$且$\left\{\begin{array}{l}0<x<1\\ 0<y<1\end{array}\right.$
面积为$\frac{π}{4}-\frac{1}{2}$,所以$\frac{m}{n}=\frac{π}{4}-\frac{1}{2}$,得π=$\frac{4m}{n}+2$.
故答案为$\frac{4m}{n}+2$.
点评 本题考查了随机模拟法求圆周率的问题,也考查了几何概率的应用问题,是综合题.

练习册系列答案
相关题目
15.设全集U=R,集合A={x|x2-1<0},B={x|x(x-2)>0},则A∩(∁uB)=( )
| A. | {x|0<x<2} | B. | {x|0<x<1} | C. | {x|0≤x<1} | D. | {x|-1<x<0} |
20.下列说法中,错误的一个是( )
| A. | 将23(10)化成二进位制数是10111(2) | |
| B. | 在空间坐标系点M(1,2,3)关于x轴的对称点为(1,-2,-3) | |
| C. | 数据:2,4,6,8的方差是数据:1,2,3,4的方差的2倍 | |
| D. | 若点A(-1,0)在圆x2+y2-mx+1=0的外部,则m>-2 |
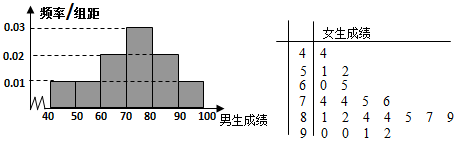
10.为了研究某学科成绩是否与学生性别有关,采用分层抽样的方法,从高二年级抽取了30名男生和20名女生的该学科成绩,得到如图所示男生成绩的频率分布直方图和女生成绩的茎叶图,规定80分以上为优分(含80分).
(Ⅰ)(i)请根据图示,将2×2列联表补充完整;
(ii)据列联表判断,能否在犯错误概率不超过10%的前提下认为“学科成绩与性别有关”?
(Ⅱ)将频率视作概率,从高二年级该学科成绩中任意抽取3名学生的成绩,求成绩为优分人数X的分布列与数学期望.
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$(n=a+b+c+d).
参考数据:

(Ⅰ)(i)请根据图示,将2×2列联表补充完整;
| 优分 | 非优分 | 总计 | |
| 男生 | |||
| 女生 | |||
| 总计 | 50 |
(Ⅱ)将频率视作概率,从高二年级该学科成绩中任意抽取3名学生的成绩,求成绩为优分人数X的分布列与数学期望.
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$(n=a+b+c+d).
参考数据:
| P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
17.设m,n是不同的直线,α,β是不同的平面,下列命题中正确的是( )
| A. | 若m∥α,n⊥β,m⊥n,则α⊥β | B. | 若m∥α,n⊥β,m∥n,则α⊥β | ||
| C. | 若m∥n,m∥α,n∥β,则α∥β | D. | 若m?α,n?α,m∥β,n∥β,则α∥β |