题目内容
15.已知函数f(x)=ex-x.(1)求f(x)的极小值;
(2)对?x∈(0,+∞),f(x)>ax恒成立,求实数a的取值范围.
分析 (1)求出函数的导数,得到函数的单调区间,求出函数的极小值即可;
(2)问题转化为$\frac{e^x}{x}-1>a$恒成立,令$g(x)=\frac{e^x}{x}-1,x>0$,求出g(x)的单调区间,求出g(x)的最小值,从而求出a的范围.
解答 解:(1)f'(x)=ex-1
| x | (-∞,0) | 0 | (0,+∞) |
| g'(x) | - | 0 | + |
| g(x) | ↘ | 极小值1 | ↗ |
(2)当x>0时,$\frac{e^x}{x}-1>a$恒成立.令$g(x)=\frac{e^x}{x}-1,x>0$,则$g'(x)=\frac{{{e^x}({x-1})}}{x^2}$,
| x | (0,1) | 1 | (1,+∞) |
| g'(x) | - | 0 | + |
| g(x) | ↘ | 极小值 | ↗ |
点评 本题考查了函数的单调性、极值问题,考查导数的应用以及函数恒成立问题,是一道中档题.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
5.已知N是自然数集,在数轴上表示出集合A,如果所示,则A∩N=( )
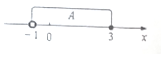

| A. | {-1,0,1,2,3} | B. | {0,1,2,3} | C. | {1,2,3} | D. | {2,3} |
10.函数f(x)=ax2+4(a+1)x-3在[2,+∞)上递减,则a的取值范围是( )
| A. | a≤-$\frac{1}{2}$ | B. | -$\frac{1}{2}$≤a<0 | C. | 0<a≤$\frac{1}{2}$ | D. | a≥$\frac{1}{2}$ |
20.下面使用类比推理正确的是( )
| A. | 由实数运算“(ab)t=a(bt)”类比到“($\overrightarrow{a}$•$\overrightarrow{b}$)•$\overrightarrow{c}$=$\overrightarrow{a}$•($\overrightarrow{b}$•$\overrightarrow{c}$)” | |
| B. | 由实数运算“(ab)t=at+bt”类比到“($\overrightarrow{a}$+$\overrightarrow{b}$)•$\overrightarrow{c}$=$\overrightarrow{a}$•$\overrightarrow{c}$+$\overrightarrow{b}$•$\overrightarrow{c}$” | |
| C. | 由实数运算“|ab|=|a||b|”类比到“|$\overrightarrow{a}$•$\overrightarrow{b}$=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|” | |
| D. | 由实数运算“$\frac{ac}{bc}$=$\frac{a}{b}$”类比到“$\frac{\overrightarrow{a}•\overrightarrow{c}}{\overrightarrow{b}•\overrightarrow{c}}$=$\frac{\overrightarrow{a}}{\overrightarrow{b}}$” |
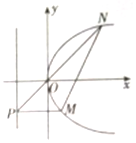 双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{3}=1(a>0)$的左、右焦点分别为F1,F2,过F2作x轴垂直的直线交双曲线C于A、B两点,△F1AB的面积为12,抛物线E:y2=2px(p>0)以双曲线C的右顶点为焦点.
双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{3}=1(a>0)$的左、右焦点分别为F1,F2,过F2作x轴垂直的直线交双曲线C于A、B两点,△F1AB的面积为12,抛物线E:y2=2px(p>0)以双曲线C的右顶点为焦点.