题目内容
7.函数y=3$\sqrt{x-1}$+4$\sqrt{2-x}$的最大值为5.分析 根据柯西不等式的性质求出函数的最大值即可.
解答 解:由柯西不等式可得:y2=(3$\sqrt{x-1}$+4$\sqrt{2-x}$)2≤(32+42)(x-1+2-x)=25,
当且仅当$\frac{\sqrt{x-1}}{3}$=$\frac{\sqrt{2-x}}{4}$时“=”成立,
故函数的最大值是5,
故答案为:5.
点评 本题考查了柯西不等式的性质,考查转化思想,是一道基础题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
2.已知函数f(x)=($\frac{1}{3}$)x,a>0,b>0,a≠b,m=f($\frac{a+b}{2}$),n=f($\sqrt{ab}$),p=f($\frac{2ab}{a+b}$),则m,n,p 的大小关系为( )
| A. | m<n<p | B. | m<p<n | C. | p<m<n | D. | p<n<m |
12.要得到函数y=sin ($\frac{π}{4}$-$\frac{x}{2}$)的图象,只需将y=cos $\frac{x}{2}$的图象( )
| A. | 向左平移$\frac{π}{2}$个单位 | B. | 向右平移$\frac{π}{2}$个单位 | ||
| C. | 向左平移$\frac{π}{4}$个单位 | D. | 向右平移$\frac{π}{4}$个单位 |
16.若|$\overrightarrow{AB}$|=5,|$\overrightarrow{AC}$|=8,则|$\overrightarrow{BC}$|的取值范围是( )
| A. | [3,8] | B. | (3,8) | C. | [3,13] | D. | (3,13) |
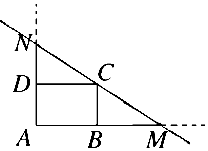 如图,已知矩形ABCD中,AB=6,AD=4,过点C的直线l与AB,AD的延长线分别交于点M,N.
如图,已知矩形ABCD中,AB=6,AD=4,过点C的直线l与AB,AD的延长线分别交于点M,N.