题目内容
17.(1)若函数f(2x+1)=x2-2x,求f(x)解析式(2)若一次函数f(x)为增函数,且f(f(x))=4x+1,求f(x)解析式.
分析 (1)利用换元法求解即可.
(2)利用待定系数法求解即可
解答 解:(1)函数f(2x+1)=x2-2x,
设2x+1=t,则x=$\frac{1}{2}$(t-1),
那么函数f(2x+1)=x2-2x转化为g(t)=$\frac{1}{4}$(t-1)2-2×$\frac{1}{2}$(t-1)=$\frac{1}{4}$t2-$\frac{3}{2}t$$+\frac{5}{4}$,
∴f(x)解析式为f(x)=$\frac{1}{4}$x2-$\frac{3}{2}x$$+\frac{5}{4}$;
(2)f(x)是一次函数且f(x)为增函数,设f(x)=kx+b,(k>0),
f(f(x))=f(kx+b)=k(kx+b)+b=4x+1,
由$\left\{\begin{array}{l}{{k}^{2}=4}\\{kb+b=1}\end{array}\right.$,解得:k=2,b=$\frac{1}{3}$,
∴f(x)解析式为$f(x)=2x+\frac{1}{3}$.
点评 本题考查了函数解析式的求法,利用了换元法和待定系数法,属于基础题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
8.设函数f(x)=Asin(ωx+φ),x∈R(其中A>0,ω>0),在($\frac{π}{6}$,$\frac{π}{2}$)上既无最大值,也无最小值,且-f($\frac{π}{2}$)=f(0)=f($\frac{π}{6}$),则下列结论成立的是 ( )
| A. | 若f(x1)≤f(x)≤f(x2)对?x∈R恒成立,则|x2-x1|min=π | |
| B. | y=f(x)的图象关于点(-$\frac{2π}{3}$,0)中心对称 | |
| C. | 函数f(x)的单调区间为:[kπ+$\frac{π}{12}$,kπ+$\frac{7π}{12}$](k∈Z) | |
| D. | 函数y=|f(x)|(x∈R)的图象相邻两条对称轴之间的距离是$\frac{π}{2}$ |
5.给出下列四个函数,其中图象关于y轴对称的是( )
| A. | y=x-5 | B. | y=$\frac{{x}^{2}+1}{x}$ | C. | y=2x+log2x | D. | y=3x+3-x |
12.已知各项均为正数的等比数列{an}满足a3•a5=64,a2=2,则a1=( )
| A. | 4 | B. | 2 | C. | 1 | D. | $\frac{1}{2}$ |
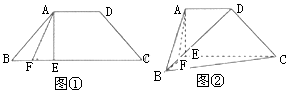 如图①所示,四边形ABCD为等腰梯形,AD∥BC,且AD=$\frac{1}{3}$BC=a,∠BAD=135°,AE⊥BC于点E,F为BE的中点.将△ABE沿着AE折起至△AB′E的位置,得到如图②所示的四棱锥B′-ADCE.
如图①所示,四边形ABCD为等腰梯形,AD∥BC,且AD=$\frac{1}{3}$BC=a,∠BAD=135°,AE⊥BC于点E,F为BE的中点.将△ABE沿着AE折起至△AB′E的位置,得到如图②所示的四棱锥B′-ADCE. 如图,平行六面体ABCDA1B1C1D1中,$\overrightarrow{AB}$=a,$\overrightarrow{AD}$=b,$\overrightarrow{A{A}_{1}}$=c,E为A1D1的中点,F为BC1与B1C的交点,
如图,平行六面体ABCDA1B1C1D1中,$\overrightarrow{AB}$=a,$\overrightarrow{AD}$=b,$\overrightarrow{A{A}_{1}}$=c,E为A1D1的中点,F为BC1与B1C的交点,