题目内容
已知函数f(x)=2x-2-4x,x∈[-4,0],求f(x)的最大值和最小值.
考点:函数的最值及其几何意义
专题:计算题,函数的性质及应用
分析:由题意,配方可得f(x)=2x-2-4x=-4x+
2x=-(2x-2-3)2+2-6,从而求最值.
| 1 |
| 4 |
解答:
解:f(x)=2x-2-4x=-4x+
2x=-(2x-2-3)2+2-6,
∵x∈[-4,0],
∴2x∈[2-4,1],
故当2x=2-3,即x=-3时,fmax(x)=2-6,
当2x=20,即x=0时,fmin(x)=
-1=-
.
| 1 |
| 4 |
∵x∈[-4,0],
∴2x∈[2-4,1],
故当2x=2-3,即x=-3时,fmax(x)=2-6,
当2x=20,即x=0时,fmin(x)=
| 1 |
| 4 |
| 3 |
| 4 |
点评:本题考查了函数的最大值及最小值的求法,利用了配方法与整体代换的方法,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若集合M={y|y=x-2},P={x|y=
},那么( )
| x-1 |
| A、M⊆P | B、P⊆M |
| C、M∩P=ϕ | D、M∪P=R |
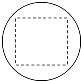 已知某一多面体内接于球构成一个组合体,如果该组合体的正视图,侧视图,俯视图均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是( )
已知某一多面体内接于球构成一个组合体,如果该组合体的正视图,侧视图,俯视图均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是( )| A、4π | B、8π |
| C、12π | D、16π |
设椭圆
+
=1的左右焦点分别为F1,F2,P是椭圆上的一动点,若△PF1F2是直角三角形,则△PF1F2的面积为( )
| x2 |
| 4 |
| y2 |
| 3 |
| A、3 | ||
B、3或
| ||
C、
| ||
| D、6或3 |