题目内容
16.在△ABC中,内角A,B,C的对边分别为a,b,c,且asinB=$\sqrt{3}$bcosA.(Ⅰ)求A;
(Ⅱ)若a=$\sqrt{7}$,c-b=1,求△ABC的面积.
分析 (Ⅰ)根据正弦定理化简可得答案.
(Ⅱ)由a=$\sqrt{7}$,c-b=1,利用余弦定理求解bc的值面积求出△ABC的面积.
解答 解:(Ⅰ)在△ABC中,∵asinB=$\sqrt{3}$bcosA.
由正弦定理,得:sinAsinB=$\sqrt{3}$sinBcosA∵0<B<π,sinB≠0.
∴sinA=$\sqrt{3}$cosA
即tanA=$\sqrt{3}$.
∵0<A<π,
∴A=$\frac{π}{3}$.
(Ⅱ)由a=$\sqrt{7}$,c-b=1,A=$\frac{π}{3}$,
由余弦定理,cosA=$\frac{{c}^{2}+{b}^{2}-{a}^{2}}{2bc}$,
得:bc=(c-b)2+2bc-7.
解得:bc=6.
∴△ABC的面积S=$\frac{1}{2}$bcsinA=$\frac{1}{2}×6×\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{2}$.
点评 本题考查三角形的正余弦定理和内角和定理的运用,考查运算能力,属于基础题.

练习册系列答案
相关题目
6.过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右顶点A作斜率为-1的直线,该直线与双曲线的两条渐近线的交点分别为B、C,若$\overrightarrow{AB}$=$\frac{1}{2}$$\overrightarrow{BC}$,则双曲线的渐近线方程为( )
| A. | y=±$\sqrt{2}$x | B. | y=±$\sqrt{3}$x | C. | y=±2x | D. | y=±$\sqrt{5}$x |
7. 如图所示,已知二面角α-l-β的平面角为θ,PA⊥α,PB⊥β,A、B为垂足,且PA=4,PB=5,设A、B到棱l的距离分别为x、y,当θ变化时,点(x,y)的轨迹是下列图形中的( )
如图所示,已知二面角α-l-β的平面角为θ,PA⊥α,PB⊥β,A、B为垂足,且PA=4,PB=5,设A、B到棱l的距离分别为x、y,当θ变化时,点(x,y)的轨迹是下列图形中的( )
 如图所示,已知二面角α-l-β的平面角为θ,PA⊥α,PB⊥β,A、B为垂足,且PA=4,PB=5,设A、B到棱l的距离分别为x、y,当θ变化时,点(x,y)的轨迹是下列图形中的( )
如图所示,已知二面角α-l-β的平面角为θ,PA⊥α,PB⊥β,A、B为垂足,且PA=4,PB=5,设A、B到棱l的距离分别为x、y,当θ变化时,点(x,y)的轨迹是下列图形中的( )| A. |  | B. |  | C. | 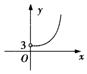 | D. |  |
11.已知f(x)=x2-x+1,g(x)=kx,则“|k|≤1”是“f (x)≥g(x) 在R上恒成立”的( )
| A. | 充分但不必要条件 | B. | 必要但不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
6. 如图,给出了样本容量均为7的A、B两组样本数据的散点图,已知A组样本数据的相关系数为r1,B组数据的相关系数为r2,则( )
如图,给出了样本容量均为7的A、B两组样本数据的散点图,已知A组样本数据的相关系数为r1,B组数据的相关系数为r2,则( )
 如图,给出了样本容量均为7的A、B两组样本数据的散点图,已知A组样本数据的相关系数为r1,B组数据的相关系数为r2,则( )
如图,给出了样本容量均为7的A、B两组样本数据的散点图,已知A组样本数据的相关系数为r1,B组数据的相关系数为r2,则( )| A. | r1=r2 | B. | r1<r2 | C. | r1>r2 | D. | 无法判定 |