题目内容
【题目】如图,在三棱柱中![]() ,点P,G分别是AD,EF的中点,已知
,点P,G分别是AD,EF的中点,已知![]() 平面ABC,AD=EF=3,DE=DF=2.
平面ABC,AD=EF=3,DE=DF=2.
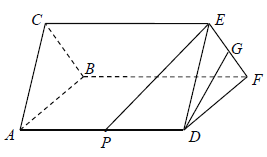
(Ⅰ)求证:DG⊥平面BCEF;
(Ⅱ)求PE与平面BCEF 所成角的正弦值.
【答案】( Ⅰ)见解析;(Ⅱ) ![]() .
.
【解析】试题分析: (Ⅰ)要证![]() 与平面
与平面![]() 垂直,就要证
垂直,就要证![]() 与平面
与平面![]() 内两条相交直线垂直,其中一条由等腰三角形的性质可得,即
内两条相交直线垂直,其中一条由等腰三角形的性质可得,即![]() ,再由已知
,再由已知![]() 平面
平面![]() ,即三棱柱侧棱与底面垂直,因此可得
,即三棱柱侧棱与底面垂直,因此可得![]() ,由此得
,由此得![]() ,从而得线面垂直;(Ⅱ)要求
,从而得线面垂直;(Ⅱ)要求![]() 与平面
与平面![]() 所成的角,一般要作出线面角,实际上要作出
所成的角,一般要作出线面角,实际上要作出![]() 在平面
在平面![]() 内的射影,即过
内的射影,即过![]() 作平面
作平面![]() 的垂线,由(Ⅰ)知
的垂线,由(Ⅰ)知![]() 平面
平面![]() ,因此想到平移
,因此想到平移![]() 到
到![]() 点位置,为此取
点位置,为此取![]() 的中点
的中点![]() ,连
,连![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,可得
,可得![]() ,即
,即![]() 平面
平面![]() ,所以
,所以![]() 就是直线
就是直线![]() 与平面
与平面![]() 所成的角,解相应直角三角形可得.
所成的角,解相应直角三角形可得.
试题解析:
(Ⅰ)证明:因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
所以![]() ,
,
因为![]() ,
,![]() 是
是![]() 的中点,所以
的中点,所以![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() ;
;

(Ⅱ)取![]() 的中点
的中点![]() ,连
,连![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() 平面
平面![]() ,
,
所以![]() 是
是![]() 与平面
与平面![]() 所成的角,
所成的角,
由已知得,![]() ,
,![]() ,
,
所以![]() .-
.-

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
【题目】某厂最近十年生产总量逐年上升,如表是部分统计数据:
年份 | 2008 | 2010 | 2012 | 2014 | 2016 |
生产总量(万吨) |
(Ⅰ)利用所给数据求年生产总量与年份之间的回归直线方程![]() ;
;
(Ⅱ)利用(Ⅰ)中所求出的直线方程预测该厂2018年生产总量.
(回归直线的方程: ![]() ,其中
,其中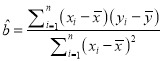 ,
, ![]() )
)