题目内容
【题目】已知向量 
=（2，1）， 
=（1，7）， 
=（5，1），设X是直线OP上的一点（O为坐标原点），那么 
的最小值是 ．
【答案】-8
【解析】解：∵X是直线OP上的点，则设X（2λ，λ）
即有 
（1﹣2λ，7﹣λ）， 
（5﹣2λ，1﹣λ）
∴ 
=（1﹣2λ）（5﹣2λ）+（7﹣λ）（1﹣λ）=5﹣2λ﹣10λ+4λ2+7﹣7λ﹣λ+λ2=5λ2﹣20λ+12
对称轴为λ=﹣（﹣20）÷（5×2）=2
∴最小值为5×2×2﹣20×2+12=﹣8
所以答案是：﹣8
【考点精析】本题主要考查了函数的最值及其几何意义的相关知识点，需要掌握利用二次函数的性质（配方法）求函数的最大（小）值；利用图象求函数的最大（小）值；利用函数单调性的判断函数的最大（小）值才能正确解答此题．
练习册系列答案
相关题目
【题目】在平面直角坐标系
中，曲线
的参数方程为
（
为参数），在以原点为极点， 
轴正半轴为极轴的极坐标系中，直线
的极坐标方程为
．
（1）求曲线
的普通方程和直线
的倾斜角；
（2）设点
，直线
和曲线
交于
两点，求
的值．
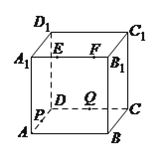
【题目】如图，正方体
的棱长为
，动点
、
在棱
上，动点
，
分别在棱
，
上，若
，
，
，
（
，
，
大于零），则四面体
的体积（ ）．
A. 与，，都有关 B. 与有关，与，无关
C. 与有关，与，无关 D. 与有关，与，无关
【题目】某科技公司生产一种手机加密芯片，其质量按测试指标划分为：指标大于或等于
为合格品，小于为次品．现随机抽取这种芯片共
件进行检测，检测结果统计如表：
测试指标 |
|
|
|
|
|
芯片数量（件） |
|
|
|
|
|
已知生产一件芯片，若是合格品可盈利
元，若是次品则亏损
元.
（Ⅰ）试估计生产一件芯片为合格品的概率；并求生产
件芯片所获得的利润不少于
元的概率.
（Ⅱ）记
为生产
件芯片所得的总利润，求随机变量
的分布列和数学期望
