题目内容
14.已知直线$\sqrt{2}$ax+by=$\sqrt{3}$(a,b是实数)与圆O:x2+y2=1(O是坐标原点)相交于A,B两点,且△AOB是等边三角形,点P(a,b)是以点M(0,$\sqrt{2}$)为圆心的圆M上的任意一点,则圆M的面积的最大值为(6+4$\sqrt{2}$)π.分析 根据圆的方程找出圆心坐标和半径,由△AOB是等边三角形得到a与b的轨迹方程为一个椭圆,圆M的面积最大时,所求半径为椭圆2a2+b2=4上点P(a,b)到焦点(0,$\sqrt{2}$)的距离最大值,即可得出结论.
解答 解:由圆x2+y2=1,所以圆心(0,0),半径为1
所以|OA|=|OB|=1,
因为△AOB是等边三角形,
所以圆心(0,0)到直线$\sqrt{2}$ax+by=$\sqrt{3}$的距离为$\frac{\sqrt{3}}{\sqrt{2{a}^{2}+{b}^{2}}}$=$\frac{\sqrt{3}}{2}$,
所以2a2+b2=4.
因此,圆M的面积最大时,所求半径为椭圆2a2+b2=4上点P(a,b)到焦点(0,$\sqrt{2}$)的距离最大值,由椭圆的性质,可知最大值为2+$\sqrt{2}$.
所以圆M的面积最大值为π(2+$\sqrt{2}$)2=(6+4$\sqrt{2}$)π.
故答案为:(6+4$\sqrt{2}$)π.
点评 本题考查学生灵活点到直线的距离公式化简求值,综合运用所学的知识求动点形成的轨迹方程,是一道综合题.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
2.已知a是第二象限角,则$\frac{a}{2}$与$\frac{π}{2}$-α都不是( )
| A. | 第一象限角 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |
6.设方程x2+x-1=0的两个实数根分别为x1、x2,则$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=( )
| A. | 1 | B. | -1 | C. | $\sqrt{5}$ | D. | $\frac{\sqrt{5}}{5}$ |
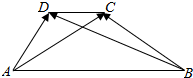 如图,梯形ABCD中,AB∥CD,AB=3CD.
如图,梯形ABCD中,AB∥CD,AB=3CD.