题目内容
3.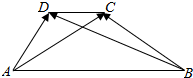 如图,梯形ABCD中,AB∥CD,AB=3CD.
如图,梯形ABCD中,AB∥CD,AB=3CD.(1)求证:$\overrightarrow{BC}$=-$\frac{2}{3}$$\overrightarrow{AB}$+$\overrightarrow{AD}$;
(2)若AB=3,AD=2,$\overrightarrow{AD}$•$\overrightarrow{BC}$=1,求$\overrightarrow{AC}$•$\overrightarrow{BD}$的值.
分析 (1)利用向量的三角形法则进行证明;
(2)将所求利用梯形的各边对应的向量表示,然后进行数量积的运算即可.
解答 (1)证明:因为梯形ABCD中,AB∥CD,AB=3CD.
所以$\overrightarrow{BC}$=$\overrightarrow{AC}-\overrightarrow{AB}$=$\overrightarrow{AD}+\overrightarrow{DC}-\overrightarrow{AB}$=$\overrightarrow{AD}+\frac{1}{3}\overrightarrow{AB}-\overrightarrow{AB}$=-$\frac{2}{3}$$\overrightarrow{AB}$+$\overrightarrow{AD}$;
(2)解:因为AB=3,AD=2,$\overrightarrow{AD}$•$\overrightarrow{BC}$=1,
则$\overrightarrow{AC}$•$\overrightarrow{BD}$=$(\overrightarrow{AB}+\overrightarrow{BC})•(\overrightarrow{BA}+\overrightarrow{AD})$=$-{\overrightarrow{AB}}^{2}$$+\overrightarrow{AB}•\overrightarrow{AD}$$+\overrightarrow{BC}•\overrightarrow{BA}+\overrightarrow{BC}•\overrightarrow{AD}$
=-9+1+$\overrightarrow{AB}•(\overrightarrow{AD}-\overrightarrow{BC})$=-8+$\overrightarrow{AB}•\frac{2}{3}\overrightarrow{AB}$=-8+6=-2.
点评 本题考查了平面向量的运算,包括加减运算和数量积运算;属于基础题.

| A. | 2+$\frac{{2\sqrt{6}}}{3}$ | B. | $\frac{{2\sqrt{6}}}{3}$ | C. | 1+$\frac{{2\sqrt{6}}}{3}$ | D. | 3 |
| A. | $[\frac{5}{4},+∞)$ | B. | $(1,\frac{5}{4}]$ | C. | $[\frac{7}{4},+∞)$ | D. | $(1,\frac{7}{4})$ |
| A. | 8 | B. | -4 | C. | 6 | D. | 无法确定 |