题目内容
9.求证:$\frac{1-2co{s}^{2}α}{sinαcosα}$=tanα-cotα分析 运用同角三角函数基本关系式和二倍角公式对等式化简,证明等式左边等于右边即可.
解答 证明:∵左边=$\frac{1-(1+cos2α)}{sinαcosα}$=-$\frac{cos2α}{sinαcosα}$,
右边=$\frac{sinα}{cosα}-\frac{cosα}{sinα}$=$\frac{si{n}^{2}α-co{s}^{2}α}{sinαcosα}$=-$\frac{cos2α}{sinαcosα}$.
∴左边=右边,得证.
点评 本题考查三角函数的化简和证明,考查同角三角函数基本关系式和二倍角公式的应用,属于基础题.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
20.已知a>b,c>d,那么一定正确的是( )
| A. | ad>bc | B. | ac>bd | C. | a-c>b-d | D. | a-d>b-c |
17.若角a的终边落在一,四象限及x轴的正半轴,则角a的集合为( )
| A. | {a|270°+k•360°<a<90°+k•360°,k∈Z} | B. | {a|-90°+k•360°<a<270°+k•360°,k∈Z} | ||
| C. | {a|-90°+k•360°<a<90°+k•360°,k∈Z} | D. | {a|-90°+k•720°<a<90°+k•720°,k∈Z} |
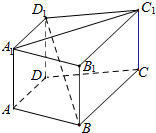 定义侧面与底面垂直的棱柱为直棱柱,在直四棱柱ABCD-A1B1C1D1中(如图),当底面四边形ABCD满足条件BD⊥AC时,有BD1⊥A1C1.
定义侧面与底面垂直的棱柱为直棱柱,在直四棱柱ABCD-A1B1C1D1中(如图),当底面四边形ABCD满足条件BD⊥AC时,有BD1⊥A1C1.