题目内容
9.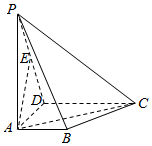 如图,ABCD是梯形,AB∥CD,∠BAD=90°,PA⊥面ABCD,且AB=1,AD=1,CD=2,PA=3,E为PD的中点.
如图,ABCD是梯形,AB∥CD,∠BAD=90°,PA⊥面ABCD,且AB=1,AD=1,CD=2,PA=3,E为PD的中点.(1)求作:AE∥平面PBC;
(2)求面PAD与面PBC所成的角.
分析 (1)取PC中点F,连接EF、BF.利用三角形中位线定理,可得EF∥DC且EF=$\frac{1}{2}DC$,结合题意得EF∥AB,且EF=AB,所以ABFE为平行四边形,可得AE∥BF,由此即得AE∥面PBC;
(2)建立以A为坐标原点,以DA,AB,AP所在的直线分别为x,y,z轴建立空间直角坐标系,求出平面的法向量,利用向量法进行求解即可.
解答 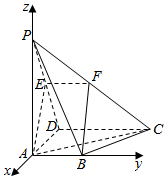 解:(1)取PC中点F,连接EF、BF.
解:(1)取PC中点F,连接EF、BF.
∵△PCD中E、F分别为PD、PC的中点,
∴EF∥DC且EF=$\frac{1}{2}DC$,
∵AB∥DC且AB=$\frac{1}{2}DC$,∴EF∥AB,且EF=AB,
∴ABFE为平行四边形,可得AE∥BF,
∵AE?面PBC,BF?面PBC,∴AE∥面PBC.
(2)∵ABCD是梯形,AB∥CD,∠BAD=90°,PA⊥面ABCD,且AB=1,AD=1,CD=2,PA=3,
∴以A为坐标原点,以DA,AB,AP所在的直线分别为x,y,z轴建立空间直角坐标系如图:
则A(0,0,0),D(-1,0,0),B(0,1,0),P(0,0,3),C(-1,2,0),
则平面PAD的法向量为$\overrightarrow{m}$=(0,1,0),
平面PBC的法向量为$\overrightarrow{n}$=(x,y,z),
则$\overrightarrow{BC}$=(-1,1,0),$\overrightarrow{BP}$=(0,-1,3)
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{BC}=-x+y=0}\\{\overrightarrow{n}•\overrightarrow{BP}=-y+3z=0}\end{array}\right.$,令z=1,则y=3,x=3.即$\overrightarrow{n}$=(3,3,1),
则cos<$\overrightarrow{m}$,$\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{3}{\sqrt{9+9+1}}=\frac{3}{\sqrt{19}}$=$\frac{3\sqrt{19}}{19}$,
即<$\overrightarrow{m}$,$\overrightarrow{n}$>=arccos$\frac{3\sqrt{19}}{19}$,
则求面PAD与面PBC所成的角为arccos$\frac{3\sqrt{19}}{19}$.
点评 本题主要考查线面平行的判定以及二面角的求解,建立空间坐标系,求出平面的法向量,利用向量法是解决二面角的常用方法.

 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案| A. | 1 | B. | 2 | C. | 3 | D. | 4 |

| A. | $s≤\frac{3}{2}$ | B. | $s≤\frac{7}{4}$ | C. | $s≤\frac{23}{12}$ | D. | $s≤\frac{49}{24}$ |
| A. | 最大值为2,周期是π | B. | 最大值为2,周期是2π | ||
| C. | 最大值为$\sqrt{2}$,周期是π | D. | 最大值为$\sqrt{2}$,周期是2π |
| A. | 身高在145.75cm以上 | B. | 身高在145.75cm左右 | ||
| C. | 身高一定是145.75cm | D. | 身高在145.75cm以下 |
| A. | p∧q是真命题 | B. | p∨q是假命题 | C. | ¬p是真命题 | D. | ¬q是真命题 |
 已知平面五边形ADCEF关于BC对称,点B在AF上(如图1),DE与BC交于点G,且AD=AB=1,CD=BC=$\sqrt{3}$,将此图形沿BC折叠成直二面角,连接AF,DE得到几何体(如图2).
已知平面五边形ADCEF关于BC对称,点B在AF上(如图1),DE与BC交于点G,且AD=AB=1,CD=BC=$\sqrt{3}$,将此图形沿BC折叠成直二面角,连接AF,DE得到几何体(如图2).