题目内容
1. 已知平面五边形ADCEF关于BC对称,点B在AF上(如图1),DE与BC交于点G,且AD=AB=1,CD=BC=$\sqrt{3}$,将此图形沿BC折叠成直二面角,连接AF,DE得到几何体(如图2).
已知平面五边形ADCEF关于BC对称,点B在AF上(如图1),DE与BC交于点G,且AD=AB=1,CD=BC=$\sqrt{3}$,将此图形沿BC折叠成直二面角,连接AF,DE得到几何体(如图2).(1)证明:平面DEG∥平面ABF;
(2)求多面体ABC-DEF的体积.
分析 (1)证明:DG∥平面ABF,GE∥平面ABF,利用平面与平面平行的判定定理证明平面DEG∥平面ABF;
(2)图(2),连接DF,GF,则多面体ABC-DEF的体积=VF-ABGD+VF-DGE.
解答  (1)证明:由平面图形,可得DG∥AB,GE∥BF,
(1)证明:由平面图形,可得DG∥AB,GE∥BF,
∵DG?平面ABF,AB?平面ABF,
∴DG∥平面ABF.
同理GE∥平面ABF.
∵DG∩GE=G,
∴平面DEG∥平面ABF;
(2)解:图(1),连接AC,则由勾股定理可得AC=2,
∴∠BCD=60°,
∴DG=$\frac{3}{2}$,BG=$\frac{\sqrt{3}}{2}$.
图(2),连接DF,GF,则多面体ABC-DEF的体积=VF-ABGD+VF-DGE=$\frac{1}{3}×\frac{1+\frac{3}{2}}{2}×\frac{\sqrt{3}}{2}×1$+$\frac{1}{3}×\frac{3}{2}×\frac{3}{2}×\frac{\sqrt{3}}{2}$=$\frac{7\sqrt{3}}{12}$.
点评 本题考查线面平行、平面与平面平行的判定,考查几何体体积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
13.已知双曲线的渐近线方程为$y=±\sqrt{2}x$,焦点坐标为$(0,-\sqrt{6})$、$(0,\sqrt{6})$,则双曲线方程为( )
| A. | $\frac{y^2}{2}-\frac{x^2}{8}=1$ | B. | $\frac{y^2}{8}-\frac{x^2}{2}=1$ | C. | $\frac{y^2}{2}-\frac{x^2}{4}=1$ | D. | $\frac{y^2}{4}-\frac{x^2}{2}=1$ |
 如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H,以下四个命题:
如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H,以下四个命题: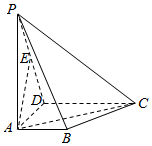 如图,ABCD是梯形,AB∥CD,∠BAD=90°,PA⊥面ABCD,且AB=1,AD=1,CD=2,PA=3,E为PD的中点.
如图,ABCD是梯形,AB∥CD,∠BAD=90°,PA⊥面ABCD,且AB=1,AD=1,CD=2,PA=3,E为PD的中点. 函数f(x)=Asin(ωx+ϕ)(A,ω,ϕ是常数,且A>0,ω>0)的部分图象如图所示,下列结论:
函数f(x)=Asin(ωx+ϕ)(A,ω,ϕ是常数,且A>0,ω>0)的部分图象如图所示,下列结论: 如图,在三棱锥A-BCD中,平面ABD和底面BCD垂直,点F是棱CD上的动点,E,O分别是AD,BD的中点,已知AB=AD=$\sqrt{2}$,BD=2CD,∠BAD=∠BDC=90°.
如图,在三棱锥A-BCD中,平面ABD和底面BCD垂直,点F是棱CD上的动点,E,O分别是AD,BD的中点,已知AB=AD=$\sqrt{2}$,BD=2CD,∠BAD=∠BDC=90°.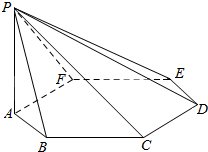 设ABCDEF是边长为1的正六边形,PA垂直于正六边形所在的平面,且PA=2.求
设ABCDEF是边长为1的正六边形,PA垂直于正六边形所在的平面,且PA=2.求