题目内容
已知sin(
+α)+cos(
-α)=
,且α∈(0,π),则
的值为 .
| π |
| 2 |
| π |
| 2 |
| 1 |
| 5 |
| 1 |
| tanα |
考点:运用诱导公式化简求值,三角函数的化简求值
专题:三角函数的求值
分析:首先根据sin2α+cos2α=1以及角的范围求出sinα和cosα的值,然后根据tanα=
求出结果.
| sinα |
| cosα |
解答:
解:∵sin(
+α)+cos(
-α)=
,且α∈(0,π),
∴cosα+sinα=
,①
∵sin2α+cos2α=1,
∴(sinα+cosα)2=1+2sinαcosα=
,
∴sinαcosα=-
,
∴(sinα-cosα)2=1+
=
,
sinα-cosα=
,②
联立①②,
sinα=
,cosα=-
,
∴tanα=-
,
故答案为:-
.
| π |
| 2 |
| π |
| 2 |
| 1 |
| 5 |
∴cosα+sinα=
| 1 |
| 5 |
∵sin2α+cos2α=1,
∴(sinα+cosα)2=1+2sinαcosα=
| 1 |
| 25 |
∴sinαcosα=-
| 12 |
| 25 |
∴(sinα-cosα)2=1+
| 24 |
| 25 |
| 49 |
| 25 |
sinα-cosα=
| 7 |
| 5 |
联立①②,
sinα=
| 4 |
| 5 |
| 3 |
| 5 |
∴tanα=-
| 4 |
| 3 |
故答案为:-
| 4 |
| 3 |
点评:此题考查了同角三角函数的基本关系,巧用sin2α+cos2α=1是解题的关键,要注意角的范围.

练习册系列答案
相关题目
已知函数f(x),g(x)均为[a,b]上的可导函数,在[a,b]上连续且f′(x)<g′(x),则f(x)-g(x)的最大值为( )
| A、f(a)-g(a) |
| B、f(b)-g(b) |
| C、f(a)-g(b) |
| D、f(b)-g(a) |
 某市为调研高三一轮复习质量,在2014年10月份组织了一次摸底考试,并从某校2015届高三理科学生在该次考试的数学成绩进行分析,利用分层抽样抽取90分以上的1200名学生的成绩进行分析,已知该样本的容量为20,分数用茎叶图记录如图所示(部分数据丢失),得到的频率分布表如下:
某市为调研高三一轮复习质量,在2014年10月份组织了一次摸底考试,并从某校2015届高三理科学生在该次考试的数学成绩进行分析,利用分层抽样抽取90分以上的1200名学生的成绩进行分析,已知该样本的容量为20,分数用茎叶图记录如图所示(部分数据丢失),得到的频率分布表如下: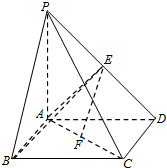 如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PA⊥底面ABCD,PA=AB=2,E,F分别为PD,AC的中点.
如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PA⊥底面ABCD,PA=AB=2,E,F分别为PD,AC的中点.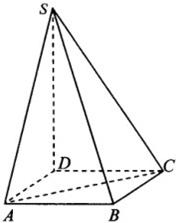 如图,设四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD,SD=2a,AD=
如图,设四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD,SD=2a,AD= 如图,写出终边落在该直线上的角的集合.
如图,写出终边落在该直线上的角的集合.