题目内容
有12名划船运动员，其中3人只会划左舷，4人只会划右舷，其余5人既会划左舷又会划右舷，现在要从这12名运动员中选出6人平均分在左、右舷划船参加比赛，则有 种不同的选法．
考点：计数原理的应用
专题：排列组合
分析：分四类，第一类 3个只会左舷的人全不选，第二类3个只会左舷的人中只选1人，第三类3个只会左舷的人中只选2人，第四类3个只会左舷的人全选，根据分类计数原理即得所求
解答：
解：分四类，第一类 3个只会左舷的人全不选，有C30C53C63=200，
第二类3个只会左舷的人中只选1人，有C31C52C73=1050，
第三类3个只会左舷的人中只选2人，有C32C51C83=840，
第四类3个只会左舷的人全选，有C33C93=84，
所以共有200+1050+840+84=2174．
故答案为：2174
第二类3个只会左舷的人中只选1人，有C31C52C73=1050，
第三类3个只会左舷的人中只选2人，有C32C51C83=840，
第四类3个只会左舷的人全选，有C33C93=84，
所以共有200+1050+840+84=2174．
故答案为：2174
点评：本题主要考查了分类计数原理，合理的分类是解决的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
若连续抛两次骰子分别所得的点数a，b作为点P的横、纵坐标，则点P在直线x+y=5下方的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
某市为调研高三一轮复习质量，在2014年10月份组织了一次摸底考试，并从某校2015届高三理科学生在该次考试的数学成绩进行分析，利用分层抽样抽取90分以上的1200名学生的成绩进行分析，已知该样本的容量为20，分数用茎叶图记录如图所示（部分数据丢失），得到的频率分布表如下：直线y=a分别与曲线y=2（x+1），y=x+lnx交于A、B，则|AB|的最小值为（ ）
| A、3 | ||||
| B、2 | ||||
C、
| ||||
D、
|
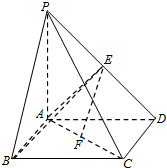如图所示，在四棱锥P-ABCD中，底面ABCD为正方形，侧棱PA⊥底面ABCD，PA=AB=2，E，F分别为PD，AC的中点．
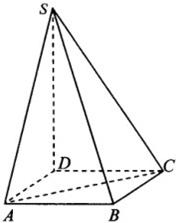如图，设四棱锥S-ABCD的底面是正方形，SD⊥平面ABCD，SD=2a，AD=