题目内容
若关于x的不等式(ax-50)lg
≤0对任意的正实数x恒成立,则实数a的取值集合是 .
| 2a |
| x |
考点:函数恒成立问题
专题:函数的性质及应用,不等式的解法及应用
分析:由题意可得a>0,x>0,设f(x)=(ax-50)lg
,可得当x无限趋近于0时,f(x)无限趋近于-∞,当x无限趋近于+∞时,f(x)无限趋近于-∞,
把f(x)≤0恒成立转化为f(x)有唯一的零点,进一步得到
=2a,由此求得a的取值集合.
| 2a |
| x |
把f(x)≤0恒成立转化为f(x)有唯一的零点,进一步得到
| 50 |
| a |
解答:
解:(ax-50)lg
≤0对任意的正实数x恒成立,
则a>0,x>0,
设f(x)=(ax-50)lg
,
当x无限趋近于0时,f(x)无限趋近于-∞,
当x无限趋近于+∞时,f(x)无限趋近于-∞,
若f(x)≤0恒成立,需f(x)有唯一的零点,
由f(x)=0,得ax-50=0或lg
=0.
解得:x=
,x=2a.
若f(x)有唯一的零点,则
=2a,
那么a2=25,即a=5.
∴实数a的取值集合是{5}.
故答案为:{5}.
| 2a |
| x |
则a>0,x>0,
设f(x)=(ax-50)lg
| 2a |
| x |
当x无限趋近于0时,f(x)无限趋近于-∞,
当x无限趋近于+∞时,f(x)无限趋近于-∞,
若f(x)≤0恒成立,需f(x)有唯一的零点,
由f(x)=0,得ax-50=0或lg
| 2a |
| x |
解得:x=
| 50 |
| a |
若f(x)有唯一的零点,则
| 50 |
| a |
那么a2=25,即a=5.
∴实数a的取值集合是{5}.
故答案为:{5}.
点评:本题考查了函数恒成立问题,考查了数学转化思想方法,把f(x)≤0恒成立转化为f(x)有唯一的零点是解答该题的关键,是中档题.

练习册系列答案
相关题目
已知函数f(x)定义域为[a,b].则“函数f(x)在[a,b]上为单调函数”是“函数f(x)在[a,b]上有最大值和最小值”的( )
| A、充分但非必要条件 |
| B、必要但非充分条件 |
| C、充要条件 |
| D、既非充分也非必要条件 |
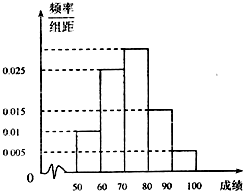 国家教育部要求高中阶段每学年都要组织学生进行“国家学生体质健康数据测试”,方案要求以学校为单位组织实施,某校对高一1班同学按照“国家学生体质健康数据测试”项目按百分制进行了测试,并对50分以上的成绩进行统计,其频率分布直方图如图所示,若90~100分数段的人数为2人.
国家教育部要求高中阶段每学年都要组织学生进行“国家学生体质健康数据测试”,方案要求以学校为单位组织实施,某校对高一1班同学按照“国家学生体质健康数据测试”项目按百分制进行了测试,并对50分以上的成绩进行统计,其频率分布直方图如图所示,若90~100分数段的人数为2人.