题目内容
已知数列 是首项为
是首项为 公比为
公比为 的等比数列,设
的等比数列,设 。
。
(1)求数列 的前n项和
的前n项和 ;
;
(2)设 ,数列
,数列 的前n项和为
的前n项和为 ,若
,若 ,是否存在正整数
,是否存在正整数 ,使得
,使得 对任意正整数
对任意正整数 恒成立?若存在,求出正整数
恒成立?若存在,求出正整数 的值或范围;若不存在,请说明理由。
的值或范围;若不存在,请说明理由。
解:(1) ,
, ,
,
当 时,
时,  ;
;
当 时,
时, 是公比为
是公比为 ,首项为
,首项为 的等比数列,
的等比数列,
 ,
,
综上 .
.
(2)由题意 ,
,
所以 ,
,
所以 ,
, .
.
则
 ,
,
即 ,所以正整数
,所以正整数 的值为
的值为 .
.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 是奇函数,且在
是奇函数,且在 内是增函数,又
内是增函数,又 ,则
,则 的解集是
的解集是 B.
B.
 D.
D.
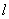 过抛物线
过抛物线 的焦点
的焦点 ,交抛物线
,交抛物线 两点,且点
两点,且点 轴的距离相等
轴的距离相等 ,则
,则 的最大值为( )
的最大值为( ) B.
B. C.4 D.6
C.4 D.6  中任取一点
中任取一点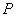 ,则点
,则点 围成的区域内(阴影部分)的概率为( )
围成的区域内(阴影部分)的概率为( ) B.
B. C.
C. D.
D.

 },则M ∩N等于( )
},则M ∩N等于( )

 B.
B. C.
C. D.
D.
 B.
B. C.
C. D.
D.