题目内容
 函数f(x)=Asin(ωx+φ),(A,ω,φ)为常数,A>0,ω>0)的部分图象如图所示,
函数f(x)=Asin(ωx+φ),(A,ω,φ)为常数,A>0,ω>0)的部分图象如图所示,(1)求f(x)的解析式;
(2)当x∈[0,
| π |
| 2 |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:(1)由图象可得A=
,由周期可得ω=2,由图象过点(
,0)可得φ=
,可得解析式;
(2)函数F(x)=f(x)-m存在零点即m=f(x)能成立,由x∈[0,
]求出函数f(x)的值域即可.
| 2 |
| π |
| 3 |
| π |
| 3 |
(2)函数F(x)=f(x)-m存在零点即m=f(x)能成立,由x∈[0,
| π |
| 2 |
解答:
解:(1)由图象可得A=
,
=
-
,解得ω=2,
又图象过点(
,0),∴2•
+φ=π,解得φ=
∴f(x)的解析式为f(x)=
sin(2x+
);
(2)函数F(x)=f(x)-m存在零点即m=f(x)能成立,
∵x∈[0,
],∴2x+
∈[
,
],
∴sin(2x+
)∈[-
,1],
∴
sin(2x+
)∈[-
,
],
∴实数m的范围为:[-
,
].
| 2 |
| 2π |
| 4ω |
| 7π |
| 12 |
| π |
| 3 |
又图象过点(
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
∴f(x)的解析式为f(x)=
| 2 |
| π |
| 3 |
(2)函数F(x)=f(x)-m存在零点即m=f(x)能成立,
∵x∈[0,
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 4π |
| 3 |
∴sin(2x+
| π |
| 3 |
| 1 |
| 2 |
∴
| 2 |
| π |
| 3 |
| ||
| 2 |
| 2 |
∴实数m的范围为:[-
| ||
| 2 |
| 2 |
点评:本题考查三角函数的图象和解析式,涉及三角函数的值域,属基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知三条直线a,b,c,两个平面α,β.则下列命题中:
①a∥c,c∥b⇒a∥b;
②a∥β,b∥β⇒a∥b;
③a∥c,c∥α⇒a∥α;
④a∥β,a∥α⇒α∥β;
⑤a?α,b∥α,a∥b⇒a∥α,
正确的命题是( )
①a∥c,c∥b⇒a∥b;
②a∥β,b∥β⇒a∥b;
③a∥c,c∥α⇒a∥α;
④a∥β,a∥α⇒α∥β;
⑤a?α,b∥α,a∥b⇒a∥α,
正确的命题是( )
| A、①⑤ | B、①② | C、②④ | D、③⑤ |
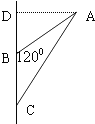 在△ABC中,AB=2,BC=1.5,∠ABC=120°(如图),若将△ABC绕直线BC旋转一周,则所形成的旋转体的体积是( )
在△ABC中,AB=2,BC=1.5,∠ABC=120°(如图),若将△ABC绕直线BC旋转一周,则所形成的旋转体的体积是( )A、
| ||
B、
| ||
C、
| ||
D、
|
设等差数列{an}的前n项和为Sn,若S3=12,S6=42,则a10+a11+a12=( )
| A、156 | B、102 |
| C、66 | D、48 |