题目内容

已知n≥2且n∈N*，对n2进行如下方式的“分拆”：22→（1，3），32→（1，3，5），42→（1，3，5，7），…，那么361的“分拆”所得的数的中位数是（　　）
A、19B、21C、29D、361
考点：归纳推理,众数、中位数、平均数
专题：计算题,推理和证明
分析：由题意可知：每个数中所分解的最大的数是前边底数的2倍减去1．则自361分裂的数中最大的数是2×19-1=37，由此得出答案即可．
解答： 解：自然数n2的分裂数中最大的数是2n-1．
361分裂的数中最大的数是2×19-1=37，
∴361的“分拆”所得的数的中位数是
1+37
2
=19．
故选：19．
点评：此题考查数字的变化规律，注意根据具体的数值进行分析分解的最大的数和底数的规律，从而推广到一般．
练习册系列答案
相关题目
i是虚数单位，记z=
i
1+i
，则|z|=（　　）
A、
1
2
+
1
2
i
B、
2
2
C、-
1
2
+
1
2
i
D、
1
2
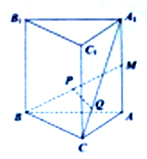在直三棱柱ABC-A1B1C1中，若BC⊥AC，∠A=
π
3
，AC=4，AA1=4，M为AA1的中点，点P为BM中点，Q在线段CA1上，且A1Q=3QC．则异面直线PQ与AC所成角的正弦值
 
．
已知数列{an}的前n项和为Sn，若4Sn=（2n-1）an+1+1（n∈N），且a1=1．
（1）求证：数列{an}为等差数列；
（2）设bn=
1
an
Sn
，数列{bn}的前n项和为Tn，证明：Tn＜
3
2
（n∈N）．
把正整数排列成如图（1）三角形数阵，檫去偶数行中的所有奇数及奇数行中的所有偶数，得到如图（2）的三角形数阵．设图（2）中的正整数按从小到大的顺序构成一个数列{an}，若ak=431，则k=
 
．
已知双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）的一个焦点与抛物线y2=20x的焦点重合，且双曲线的离心率等于
5
3
，则该双曲线的方程为
 
．
已知双曲线x2-
y2
b2
=1（b＞0）的离心率
10
，则b等于（　　）
A、2B、3C、4D、5
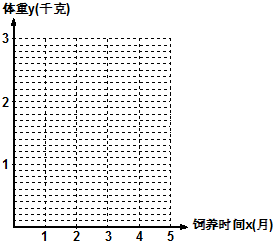某学校一个生物兴趣小组对学校的人工湖中养殖的某种鱼类进行观测研究，在饲料充足的前提下，兴趣小组对饲养时间x（单位：月）与这种鱼类的平均体重y（单位：千克）得到一组观测值，如下表：
xi（月）12345
yi（千克）0.50.91.72.12.8
（1）在给出的坐标系中，画出关于x，y两个相关变量的散点图．
（2）请根据上表提供的数据，用最小二乘法求出变量y关于变量x的线性回归直线方程
?
y
=
b
x+
?
a
．
（3）预测饲养满12个月时，这种鱼的平均体重（单位：千克）
（参考公式：
b
=
n
i=1
xiyi-n
.
x
.
y
n
i=1
x
2
i
-n(
.
x
)2
，
?
a
=
.
y
-
b
.
x
）
求过点A（-1，3），B（4，2），且在x轴、y轴上的四个截距之和是4的圆的标准方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网