题目内容
16.在△ABC中,A=$\frac{π}{3}$,AB=2,且△ABC的面积为$\frac{\sqrt{3}}{2}$,则边AC的长为1.分析 利用三角形面积公式即可得解.
解答 解:∵A=$\frac{π}{3}$,AB=2,且△ABC的面积为$\frac{\sqrt{3}}{2}$,
∴由三角形面积公式可得:S=$\frac{1}{2}$×AB×AC×sinA可得:$\frac{\sqrt{3}}{2}$=$\frac{1}{2}$×2×AC×sin$\frac{π}{3}$,
∴解得:AC=1.
故答案为:1.
点评 本题主要考查了三角形面积公式的应用,属于基础题.

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目
7.在数列{an}中,a1=1,anan-1=an-1+(-1)n(n≥2,n∈N*),则$\frac{a_3}{a_4}$的值是( )
| A. | $\frac{15}{16}$ | B. | $\frac{15}{8}$ | C. | $\frac{1}{6}$ | D. | $\frac{3}{8}$ |
1.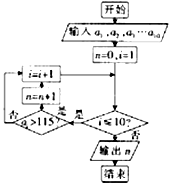 某旅游景点统计了今年5月1号至10号每天的门票收入(单位:万元),分别记为a1,a2,…,a10(如:a3表示5月3号的门票收入),表是5月1号到5月10号每天的门票收入,根据表中数据,下面程序框图输出的结果为( )
某旅游景点统计了今年5月1号至10号每天的门票收入(单位:万元),分别记为a1,a2,…,a10(如:a3表示5月3号的门票收入),表是5月1号到5月10号每天的门票收入,根据表中数据,下面程序框图输出的结果为( )
 某旅游景点统计了今年5月1号至10号每天的门票收入(单位:万元),分别记为a1,a2,…,a10(如:a3表示5月3号的门票收入),表是5月1号到5月10号每天的门票收入,根据表中数据,下面程序框图输出的结果为( )
某旅游景点统计了今年5月1号至10号每天的门票收入(单位:万元),分别记为a1,a2,…,a10(如:a3表示5月3号的门票收入),表是5月1号到5月10号每天的门票收入,根据表中数据,下面程序框图输出的结果为( )| 日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 门票收入(万元) | 80 | 120 | 110 | 91 | 65 | 77 | 131 | 116 | 55 | 77 |
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
5.下列说法正确的是( )
| A. | 零向量没有方向 | B. | 单位向量都相等 | ||
| C. | 任何向量的模都是正实数 | D. | 共线向量又叫平行向量 |
6.已知tanα=-$\frac{3}{4},且α∈(\frac{3π}{2},2π),则cos(\frac{π}{2}+α)的值是$( )
| A. | $-\frac{3}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $-\frac{4}{5}$ |
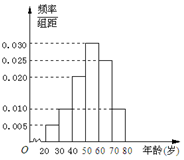 广场舞是现代城市群众文化、娱乐发展的产物,也是城市精神文明建设成果的一个重要象征.2016年某校社会实践小组对某小区广场舞的开展状况进行了年龄的调查,随机抽取了40名广场舞者进行调查,将他们年龄分成6段:[20,30),[30,40),[40,50),[50,60),[60,70),[70,80]后得到如图所示的频率分布直方图.
广场舞是现代城市群众文化、娱乐发展的产物,也是城市精神文明建设成果的一个重要象征.2016年某校社会实践小组对某小区广场舞的开展状况进行了年龄的调查,随机抽取了40名广场舞者进行调查,将他们年龄分成6段:[20,30),[30,40),[40,50),[50,60),[60,70),[70,80]后得到如图所示的频率分布直方图.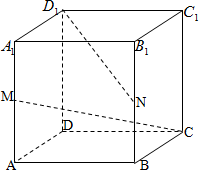 正方体ABCD-A1B1C1D1中,M、N分别为棱A1A和B1B的中点.求:
正方体ABCD-A1B1C1D1中,M、N分别为棱A1A和B1B的中点.求: