题目内容
1.将4个不同的小球装入4个不同的盒子,则在至少一个盒子为空的条件下,恰好有两个盒子为空的概率是$\frac{21}{58}$.分析 将4个不同的小球装入4个不同的盒子,分别求出恰好有一个盒子为空的基本事件、恰好有两个盒子为空的基本事件、恰好有三个盒子为空的基本事件的个数,由此能求出在至少一个盒子为空的条件下,恰好有两个盒子为空的概率.
解答 解:将4个不同的小球装入4个不同的盒子,
恰好有一个盒子为空的基本事件有:${C}_{4}^{2}•\frac{{C}_{2}^{1}{C}_{1}^{1}}{{A}_{2}^{2}}•{A}_{3}^{3}$=144,
恰好有两个盒子为空的基本事件有:$({C}_{4}^{1}{C}_{3}^{3}+\frac{{C}_{4}^{2}{C}_{2}^{2}}{{A}_{2}^{2}})•{A}_{4}^{2}$=84,
恰好有三个盒子为空的基本事件有:${A}_{4}^{1}$=4,
∴在至少一个盒子为空的条件下,恰好有两个盒子为空的概率是:
p=$\frac{84}{144+84+4}$=$\frac{21}{58}$.
故答案为:$\frac{21}{58}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
16.在单位圆中,150°的圆心角所对的弧长为( )
| A. | $\frac{2π}{3}$ | B. | $\frac{3π}{4}$ | C. | $\frac{5π}{6}$ | D. | π |
6.已知tanα=-$\frac{3}{4},且α∈(\frac{3π}{2},2π),则cos(\frac{π}{2}+α)的值是$( )
| A. | $-\frac{3}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $-\frac{4}{5}$ |
13.已知m,n是两条不同直线,α,β是两个不同平面,则下列命题中假命题的是( )
| A. | 若m⊥α,m⊥β则α∥β | B. | 若m∥n,m⊥α,则n⊥α | ||
| C. | 若m∥α,α∩β=n,则m∥n | D. | 若m⊥α,m?β则 α⊥β |
10.某几何体的三视图如图所示,则该几何体的表面积为( )
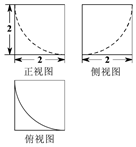

| A. | $8-\frac{4}{3}π$ | B. | $8-\frac{2}{3}π$ | C. | 24-π | D. | 24+π |
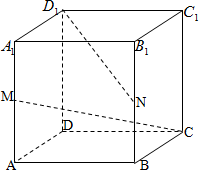 正方体ABCD-A1B1C1D1中,M、N分别为棱A1A和B1B的中点.求:
正方体ABCD-A1B1C1D1中,M、N分别为棱A1A和B1B的中点.求: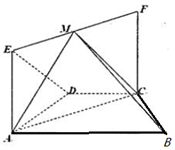 如图,在等腰梯形ABCD中,AB∥CD,AD=DC=CB=2,∠ABC=60°,四边形ACFE为矩形,CF=$\sqrt{3}$,平面ACFE⊥平面ABCD,点M为线段EF中点.
如图,在等腰梯形ABCD中,AB∥CD,AD=DC=CB=2,∠ABC=60°,四边形ACFE为矩形,CF=$\sqrt{3}$,平面ACFE⊥平面ABCD,点M为线段EF中点.