题目内容
20.若函数f(x)=-x-log2$\frac{2+ax}{2-x}$为奇函数,则使不等式f($\frac{1}{m}$)+log26<0成立的m的取值范围是( )| A. | (-∞,1) | B. | ($\frac{1}{2}$,1) | C. | (-∞,0)∪(0,1) | D. | (1,+∞) |
分析 利用函数f(x)=-x-log2$\frac{2+ax}{2-x}$为奇函数,求出a,不等式f($\frac{1}{m}$)+log26<0,即不等式f($\frac{1}{m}$)<f(1),f(x)=-x-log2$\frac{2+x}{2-x}$在(-2,2)上单调递减,即可求出m的取值范围.
解答 解:∵函数f(x)=-x-log2$\frac{2+ax}{2-x}$为奇函数,
∴f(-x)=-f(x),即x-log2$\frac{2-ax}{2+x}$=x+log2$\frac{2+ax}{2-x}$
∴a=1,
不等式f($\frac{1}{m}$)+log26<0,即不等式f($\frac{1}{m}$)<f(1),
∵f(x)=-x-log2$\frac{2+x}{2-x}$在(-2,2)上单调递减,
∴2>$\frac{1}{m}$>1,
∴$\frac{1}{2}$<m<1,
故选B.
点评 本题考查奇函数的性质,考查函数的单调性,考查学生解不等式的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.若至少存在一个x≥0,使得关于x的不等式x2≤4-|2x+m|成立,则实数m的取值范围是( )
| A. | [-4,5] | B. | [-5,5] | C. | [4,5] | D. | [-5,4] |
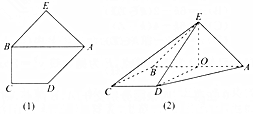 如图(1),在五边形BCDAE中,CD∥AB,∠BCD=90°,CD=BC=1,AB=2,△ABE是以AB为斜边的等腰直角三角形,现将△ABE沿AB折起,使平面ABE⊥平面ABCD,如图(2),记线段AB的中点为O.
如图(1),在五边形BCDAE中,CD∥AB,∠BCD=90°,CD=BC=1,AB=2,△ABE是以AB为斜边的等腰直角三角形,现将△ABE沿AB折起,使平面ABE⊥平面ABCD,如图(2),记线段AB的中点为O.
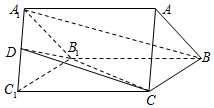 如图,在三棱柱ABC-A1B1C1中,△ABC是等边三角形,BC=CC1,D是A1C1中点.
如图,在三棱柱ABC-A1B1C1中,△ABC是等边三角形,BC=CC1,D是A1C1中点.