题目内容
以正方体的任意4个顶点为顶点的几何形体有
①空间四边形;
②每个面都是等边三角形的四面体;
③最多三个面是直角三角形的四面体;
④有三个面为等腰直角三角形,有一个面为等边三角形的四面体.
①空间四边形;
②每个面都是等边三角形的四面体;
③最多三个面是直角三角形的四面体;
④有三个面为等腰直角三角形,有一个面为等边三角形的四面体.
考点:棱柱的结构特征
专题:空间位置关系与距离
分析:找出正方体中的四面体的各种图形,例如正四面体,即可判断①②④的正误;画出图形如图即可判断③的正误,推出选项.
解答:
解:在正方体上任意选择4个顶点,由这4个顶点可能构成如下几何体: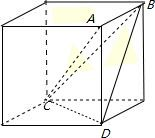
在①中,如图中的四边形ABCD,就是空间四边形,故①正确;
在②中,每个面都是等边三角形的四面体,
去掉4个角的正四面体即可,故②正确;
在③中,最多三个面是直角三角形的四面体.如图中ABCD即可,故③正确;
在④中,有三个面为全等的等腰直角三角形,有一个面为等边三角形的四面体,
去掉4个角的正四面体即可,故④正确.
故答案为:①②③④.

在①中,如图中的四边形ABCD,就是空间四边形,故①正确;
在②中,每个面都是等边三角形的四面体,
去掉4个角的正四面体即可,故②正确;
在③中,最多三个面是直角三角形的四面体.如图中ABCD即可,故③正确;
在④中,有三个面为全等的等腰直角三角形,有一个面为等边三角形的四面体,
去掉4个角的正四面体即可,故④正确.
故答案为:①②③④.
点评:本题考查命题真假的判断,考查正方体的结构特征,考查空间想象能力,是基础题.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
若(x+1)5=a0+a1(x-1)+a2(x-1)2+…+a5(x-1)5,则-a0+a1-a2+a3-a4+a5=( )
| A、0 | B、1 | C、-1 | D、-32 |
在空间四边形ABCD中,E,F分别为边AB,AD上的点,且AE:EB=AF:FD=1:4,又H,G分别为BC,CD的中点,则( )
| A、BD∥平面EFG,且四边形EFGH是矩形 |
| B、EF∥平面BCD,且四边形EFGH是梯形 |
| C、HG∥平面ABD,且四边形EFGH是菱形 |
| D、EH∥平面ADC,且四边形EFGH是平行四边形 |
 如图,在正三棱锥S-ABC中,M是侧棱SC的中点,且AB=3,SA=
如图,在正三棱锥S-ABC中,M是侧棱SC的中点,且AB=3,SA=| 10 |
| A、30° | B、45° |
| C、60° | D、以上都不是 |
某单位有7个连在一起的车位,现有3辆不同型号的车需要停放,如果要求剩余的四个空位连在一起,则不同的停车方法有( )
| A、4种 | B、16种 |
| C、18种 | D、24种 |