题目内容
新定义运算
=ad-bc，函数f（x）=
，下列命题正确的是（ ）
|
|
| A、函数f（x）是周期为π的偶函数 | ||
| B、函数f（x）是周期为2π的偶函数 | ||
C、函数f（x）是向右平移
| ||
D、函数f（x）是向左平移
|
考点：命题的真假判断与应用
专题：新定义,三角函数的图像与性质
分析：由题意，化简f（x），得出f（x）是周期为2π的非奇非偶的函数，判定A、B错误；
把f（x）的图象向右平移
，得到函数y=2cosx的图象，判定C正确；
把f（x）的图象向左平移
，得到函数y=2cos（x+
）的图象，判定D错误．
把f（x）的图象向右平移
| π |
| 3 |
把f（x）的图象向左平移
| π |
| 3 |
| 2π |
| 3 |
解答：
解：根据题意，f（x）=cosx-
sinx=2（
cosx-
sinx）=2cos（x+
），
∴f（x）是周期为2π的非奇非偶的函数，故A、B错误；
又∵f（x）的图象向右平移
，得到函数y=2cosx的图象，它是偶函数，∴C正确；
当f（x）的图象向左平移
时，得到函数y=2cos（x+
）的图象，它是非奇非偶的函数，∴D错误．
综上，正确的命题是C．
故选：C．
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
∴f（x）是周期为2π的非奇非偶的函数，故A、B错误；
又∵f（x）的图象向右平移
| π |
| 3 |
当f（x）的图象向左平移
| π |
| 3 |
| 2π |
| 3 |
综上，正确的命题是C．
故选：C．
点评：本题考查了新定义的三角函数的应用问题，解题的关键是根据新定义求出函数f（x）的解析式，是综合题目．
练习册系列答案
相关题目
计算∫
cosxdx=（ ）
0 |
| A、-1 | ||
| B、1 | ||
C、
| ||
| D、0 |
下列命题中的假命题是（ ）
| A、以矩形的一边所在直线为旋转轴，其余三边旋转形成的曲面所围成的旋转体叫圆柱 |
| B、以直角三角形的一条边所在的直线为旋转轴，其余两边旋转形成的曲面的旋转体叫圆锥 |
| C、以直角三角形的一条直角边所在直线为旋转轴，其余两边旋转形成的曲面围成的旋转体叫圆锥 |
| D、以等腰三角形的底边上的高所在直线为旋转轴，其余各边旋转形成的曲面围成的旋转体叫圆锥 |
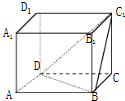如图长方体ABCD-A1B1C1D1中，AB=AD=2