题目内容
16.已知抛物线C:y2=4x,焦点为F,过点P(-1,0)作斜率为k(k>0)的直线l与抛物线C交于A,B两点,直线AF,BF分别交抛物线C于M,N两点,若$\frac{|AF|}{|FM|}$+$\frac{|BF|}{|FN|}$=18,则k=$\frac{\sqrt{5}}{5}$.分析 由题意,图形关于x轴对称,A,B,P三点共线,可得$\frac{{y}_{1}}{{x}_{1}+1}$=$\frac{{y}_{2}}{{x}_{2}+1}$.由焦半径公式|AF|=x1+1=|NF|,||BF|=x2+1=|MF|,$\frac{|AF|}{|FM|}$+$\frac{|BF|}{|FN|}$=$\frac{{y}_{1}}{{y}_{2}}$+$\frac{{y}_{2}}{{y}_{1}}$=18,(y1+y2)2=20y1y2,再利用韦达定理,即可得出结论.
解答 解:由题意,图形关于x轴对称,A,B,P三点共线,可得$\frac{{y}_{1}}{{x}_{1}+1}$=$\frac{{y}_{2}}{{x}_{2}+1}$.
由焦半径公式|AF|=x1+1=|NF|,||BF|=x2+1=|MF|,
∴$\frac{|AF|}{|FM|}$+$\frac{|BF|}{|FN|}$=$\frac{{y}_{1}}{{y}_{2}}$+$\frac{{y}_{2}}{{y}_{1}}$=18,∴(y1+y2)2=20y1y2,
由$\left\{\begin{array}{l}{{y}^{2}=4x}\\{y=k(x+1)}\end{array}\right.$,可得ky2-4y+4k=0,
∴y1+y2=$\frac{4}{k}$,y1y2=4,∴$\frac{16}{{k}^{2}}$=80,
∵k>0,∴k=$\frac{\sqrt{5}}{5}$.
故答案为$\frac{\sqrt{5}}{5}$.
点评 本题考查直线与抛物线的位置关系,考查韦达定理的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
4.x>1是“x>2”的( )
| A. | 充要条件 | B. | 必要条件 | ||
| C. | 必要非充分条件 | D. | 既非充分又非必要条件 |
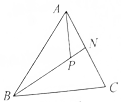 如图,在△ABC中,已知$\overrightarrow{AN}$=$\frac{1}{2}\overrightarrow{AC}$,P是BN上一点,若$\overrightarrow{AP}=m\overrightarrow{AB}+\frac{1}{4}\overrightarrow{AC}$,则实数m的值是$\frac{1}{2}$.
如图,在△ABC中,已知$\overrightarrow{AN}$=$\frac{1}{2}\overrightarrow{AC}$,P是BN上一点,若$\overrightarrow{AP}=m\overrightarrow{AB}+\frac{1}{4}\overrightarrow{AC}$,则实数m的值是$\frac{1}{2}$.