题目内容
19.在区间$[{-\frac{π}{6}\;\;,\;\;\frac{π}{2}}]$上随机地取一个数x,则事件“$sinx≥\frac{1}{2}$”发生的概率为$\frac{1}{2}$.分析 根据几何概型的概率公式进行求解即可.
解答 解:在区间$[{-\frac{π}{6}\;\;,\;\;\frac{π}{2}}]$上随机地取一个数x,事件“$sinx≥\frac{1}{2}$”,得$\frac{π}{6}$≤x≤$\frac{π}{2}$,
则事件“$sinx≥\frac{1}{2}$”发生的概率为P=$\frac{\frac{π}{2}-\frac{π}{6}}{\frac{π}{2}+\frac{π}{6}}$=$\frac{1}{2}$,
故答案为$\frac{1}{2}$.
点评 本题主要考查几何概型的概率的计算,根据三角函数的性质进行求解以及几何概型的概率公式是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.某大学生从全校学生中随机选取100名统计他们的鞋码大小,得到如下数据:
(1)某鞋店计划采购某种款式的女鞋1000双,则其中38号鞋应有多少双?
(2)完成频率分布直方图,并估计该校学生的平均鞋码.
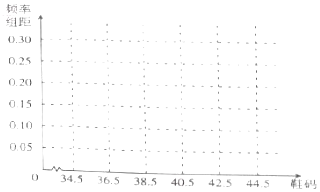
| 鞋码 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 合计 |
| 男生 | - | - | 3 | 6 | 8 | 11 | 12 | 6 | 7 | 2 | 55 |
| 女生 | 4 | 6 | 12 | 9 | 9 | 2 | 2 | - | - | 1 | 45 |
(2)完成频率分布直方图,并估计该校学生的平均鞋码.

4.设变量x,y满足约束条件$\left\{\begin{array}{l}2x-y-2≤0\\ 2x+y-2≥0\\ x+2y-4≤0\end{array}\right.$,则x2+y2的最小值为( )
| A. | 0 | B. | $\frac{4}{5}$ | C. | 1 | D. | $\sqrt{2}$ |
11.已知直线x-y+2=0与圆C:(x-3)2+(y-3)2=4(圆心为C)交于点A,B,则∠ACB的大小为( )
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
9.若复数$\frac{1-bi}{2+i}$=$\frac{1}{2}$(i是虚数单位,b是实数),则b=( )
| A. | -2 | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |