题目内容
10. 已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,-π<φ≤π)的图象如图所示,则函数f(x)的解析式为2sin($\frac{11}{6}$x-$\frac{5π}{6}$).
已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,-π<φ≤π)的图象如图所示,则函数f(x)的解析式为2sin($\frac{11}{6}$x-$\frac{5π}{6}$).
分析 根据函数图象确定A,ω和φ的值即可得到结论.
解答 解:由图象知A=2,由图象知f(0)=-1,即f(0)=2sinφ=-1,
即sinφ=-$\frac{1}{2}$,
∵-π<φ≤π,∴φ=-$\frac{π}{6}$或φ=-$\frac{5π}{6}$,
∵函数的周期T∈(π,$\frac{3π}{2}$),即π<$\frac{2π}{ω}$<$\frac{3π}{2}$,
∴$\frac{4}{3}$<ω<2,
①若φ=-$\frac{π}{6}$,则f(x)=2sin(ωx-$\frac{π}{6}$),
由f(π)=2sin(ωπ-$\frac{π}{6}$)=0,
得ωπ-$\frac{π}{6}$=kπ,
则ω=k+$\frac{1}{6}$,此时ω不存在.
②若φ=-$\frac{5π}{6}$,则f(x)=2sin(ωx-$\frac{5π}{6}$),
由f(π)=2sin(ωπ-$\frac{5π}{6}$)=0,
得ωπ-$\frac{5π}{6}$=kπ,
则ω=k+$\frac{5}{6}$,则ω=$\frac{11}{6}$,
则f(x)=2sin($\frac{11}{6}$x-$\frac{5π}{6}$),
故答案为:f(x)=2sin($\frac{11}{6}$x-$\frac{5π}{6}$).
点评 本题主要考查三角函数解析式的求解,根据条件建立方程关系,利用五点对应法是解决本题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
20.直线2x+y-7=0与直线x+2y-5=0的交点是( )
| A. | (3,-1) | B. | (-3,1) | C. | (-3,-1) | D. | (3,1) |
19.直线y=$\frac{1}{2}$x+b是曲线y=lnx(x>0)的一条切线,则实数b=( )
| A. | ln2+1 | B. | ln2-1 | C. | ln3+1 | D. | ln3-1 |
20.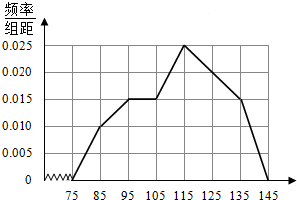 某同学将全班某次数学考试成绩整理成频率分布直方图后,并将每个小矩形上方线段的中点连接起来得到频率分布折线图(如图所示),据此估计此次考试成绩的众数是( )
某同学将全班某次数学考试成绩整理成频率分布直方图后,并将每个小矩形上方线段的中点连接起来得到频率分布折线图(如图所示),据此估计此次考试成绩的众数是( )
 某同学将全班某次数学考试成绩整理成频率分布直方图后,并将每个小矩形上方线段的中点连接起来得到频率分布折线图(如图所示),据此估计此次考试成绩的众数是( )
某同学将全班某次数学考试成绩整理成频率分布直方图后,并将每个小矩形上方线段的中点连接起来得到频率分布折线图(如图所示),据此估计此次考试成绩的众数是( )| A. | 100 | B. | 110 | C. | 115 | D. | 120 |