题目内容
19．直线y=$\frac{1}{2}$x+b是曲线y=lnx（x＞0）的一条切线，则实数b=（ ）| A． | ln2+1 | B． | ln2-1 | C． | ln3+1 | D． | ln3-1 |
分析 利用求导法则求出曲线方程的导函数解析式，由已知直线为曲线的切线，根据切线斜率求出切点坐标，代入直线解析式求出b的值即可．
解答 解：求导得：y′=$\frac{1}{x}$，
∵直线y=$\frac{1}{2}$x+b是曲线y=lnx（x＞0）的一条切线，
∴$\frac{1}{x}$=$\frac{1}{2}$，即x=2，
把x=2代入曲线方程得：y=ln2，
把切点（2，ln2）代入直线方程得：ln2=1+b，
解得：b=ln2-1，
故选：B．
点评 此题考查了利用导师研究曲线上某点的切线方程，熟练掌握导数的几何意义是解本题的关键．
练习册系列答案
周周清检测系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
9．已知x＞0，2＜x2+x＜$\frac{5}{2}$，则下列不正确的是 （ ）
| A． | cos（x-1）＜sin$\frac{π}{2}$x | B． | sin2x＜sinx2 | C． | sinx2＜cos（x-1） | D． | sin2x＞sin（2-x） |
已知函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，-π＜φ≤π）的图象如图所示，则函数f（x）的解析式为2sin（$\frac{11}{6}$x-$\frac{5π}{6}$）．
4．如图，网格纸上小正方形的边长为1，粗线画出的是某个四面体的三视图，则该四面体的表面积为（ ）
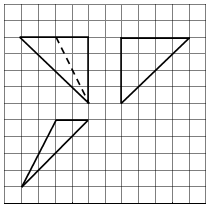
| A． | 8+8$\sqrt{2}$+4$\sqrt{6}$ | B． | 8+8$\sqrt{2}$+2$\sqrt{6}$ | C． | 2+2$\sqrt{2}$+$\sqrt{6}$ | D． | $\frac{1}{2}$+$\frac{\sqrt{2}}{2}$+$\frac{\sqrt{6}}{4}$ |
11．设函数f（x）=a1nx+$\frac{1-a}{2}$x2-x（a∈R且a≠1），若?x0∈[1，+∞），使得f（x0）＜$\frac{a}{a-1}$，则a的取值范围为（ ）
| A． | （-$\sqrt{2}-$1，$\sqrt{2}-1$） | B． | （-$\sqrt{2}-1$，1） | C． | （1，+∞） | D． | （-$\sqrt{2}-1$，$\sqrt{2}-1$）∪（1，+∞） |