题目内容
15．已知函数f（x）=（x+1）lnx-a（x+1）（a∈R），求函数g（x）=f′（x）-$\frac{a}{x}$的单调区间．分析 由f（x）求导，确定出g（x），对g（x）求导，对a进行讨论，分情况来看单调区间．
解答 解：∵f（x）=（x+1）lnx-a（x+1），定义域为（0，+∞），
∴f′（x）=lnx+1+$\frac{1}{x}$-a，
∴g（x）=lnx+1-a+$\frac{1-a}{x}$，定义域为（0，+∞），
∵g′（x）=$\frac{x-（1-a）}{{x}^{2}}$，
①a≥1时，g′（x）≥0恒成立，
∴g（x）在（0，+∞）上单调递增，
②a＜1时，g′（x）=0得x=1-a，
∴g（x）在区间（0，1-a）上单调递减，
在区间（1-a，+∞）上单调递增，
综上所述：a≥1时，g（x）的单调增区间是（0，+∞），
a＜1时，g（x）的单调增区间是（1-a，+∞），
单调减区间是（0，1-a）．
点评 本题考查分类讨论来看单调区间，时高考题目中经常考查的点．
练习册系列答案
相关题目
已知抛物线C：x2=4y的焦点为F，准线与y轴的交点为Q，过点Q的直线l与抛物线C相交于不同的A，B两点．
6．已知p：2+3=5，q：5＜4，则下列判断错误的是（ ）
| A． | “p或q”为真，“非p”为假 | B． | “p且q”为假，“非q”为真 | ||
| C． | “p且q”为假，“非p”为假 | D． | “p且q”为真，“p或q”为真 |
3．若f（x）在[a，b]上连续，则下列说法正确的是（ ）
| A． | f（x）在[a，b]上可导 | |
| B． | ${∫}_{a}^{x}$f（t）dt为f（x）在[a，b]上的一个原函数： | |
| C． | ${∫}_{x}^{b}$f（t）dt为f（x）在[a，b]上的一个原函数 | |
| D． | f（x）在[a，b]上至少有一个零点 |
已知函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，-π＜φ≤π）的图象如图所示，则函数f（x）的解析式为2sin（$\frac{11}{6}$x-$\frac{5π}{6}$）．
4．如图，网格纸上小正方形的边长为1，粗线画出的是某个四面体的三视图，则该四面体的表面积为（ ）
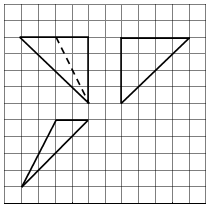
| A． | 8+8$\sqrt{2}$+4$\sqrt{6}$ | B． | 8+8$\sqrt{2}$+2$\sqrt{6}$ | C． | 2+2$\sqrt{2}$+$\sqrt{6}$ | D． | $\frac{1}{2}$+$\frac{\sqrt{2}}{2}$+$\frac{\sqrt{6}}{4}$ |