题目内容
19.如表提供了工厂技术改造后某种型号设备的使用年限x和所支出的维修费用y(万元)的几组对照数据:| x(年) | 3 | 4 | 5 | 6 |
| y(万元) | 2.5 | 3 | 4 | 4.5 |
(2)已知工厂技改前该型号设备使用10年的维修费用为9万元.试根据(1)求出的线性回归方程,预测该型号设备技改后使用10年的维修费用比技改前降低多少?
参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=y-$\stackrel{∧}{b}$x.
分析 (1)计算平均数$\overline{x}$、$\overline{y}$,求出回归系数,写出回归方程;
(2)利用回归方程求出x=10时$\stackrel{∧}{y}$的值即可.
解答 解:(1)计算$\sum_{i=1}^{4}$xiyi=3×2.5+4×3+5×4+6×4.5=66.5,
$\sum_{i=1}^4{X_i^2}={3^2}+{4^2}+{5^2}+{6^2}=86$,…(3分)
$\overline{x}$=$\frac{1}{4}$×(3+4+5+6)=4.5,
$\overline{y}$=$\frac{1}{4}$×(2.5+3+4+4.5)=3.5;…(5分)
回归系数$\hat b=\frac{66.5-4×4.5×3.5}{{86-4×{{4.5}^2}}}=\frac{66.5-63}{86-81}=0.7$;
$\hat a=\bar Y-\hat b\overline{X}=3.5-0.7×4.5=0.35$;
故所求的回归方程为$\hat y=0.7x+0.35$;…(9分)
(2)当x=10时,利用y关于x的线性回归方程计算$\stackrel{∧}{y}$=0.7×10+0.35=7.35,…(10分)
预测该型号设备技改后使用10年的维修费用比技改前降低9-7.35=1.65(万元),
答:求出y关于x的线性回归方程$\stackrel{∧}{y}$=0.7x+0.35,
预测该型号设备技改后使用10年的维修费用比技改前降低1.65万元.…(12分)
点评 本题考查了线性回归方程的应用问题,是基础题.

练习册系列答案
相关题目
19.凸十边形的对角线的条数为( )
| A. | 10 | B. | 35 | C. | 45 | D. | 90 |
20.设a,b,c的平均数为M,a与b的平均数为N,N与c的平均数为P,若a>b>c,则M与P的大小关系是( )
| A. | M=P | B. | M>P | C. | M<P | D. | 不能确定 |
14.如图所示的程序框图,若输入m=8,n=3,则输出的S值为( )
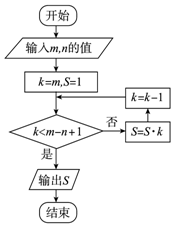

| A. | 56 | B. | 336 | C. | 360 | D. | 1440 |
8.已知函数f(x)=3x+sinx-2cosx的图象在点A(x0,f(x0))处的切线斜率为3,则tanx0的值是( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\sqrt{3}$ | D. | $-\sqrt{3}$ |