题目内容
8.已知函数f(x)=3x+sinx-2cosx的图象在点A(x0,f(x0))处的切线斜率为3,则tanx0的值是( )| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\sqrt{3}$ | D. | $-\sqrt{3}$ |
分析 由题意,求导f′(x)=3+cosx+2sinx,从而得f′(x0)=3+cosx0+2sinx0=3,从而解得tanx0的值.
解答 解:由题意,
f′(x)=3+cosx+2sinx;
∵函数f(x)=3x+sinx-2cosx的图象在点A(x0,f(x0))处的切线斜率为3,
∴f′(x0)=3+cosx0+2sinx0=3;
∴cosx0+2sinx0=0,
∴tanx0=-$\frac{1}{2}$,
故选:B.
点评 本题考查了求导及导数的几何意义,同时考查了三角函数的转化,属于基础题.

练习册系列答案
相关题目
19.如表提供了工厂技术改造后某种型号设备的使用年限x和所支出的维修费用y(万元)的几组对照数据:
(1)若知道y对x呈线性相关关系,请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\stackrel{∧}{y}$=bx+a
(2)已知工厂技改前该型号设备使用10年的维修费用为9万元.试根据(1)求出的线性回归方程,预测该型号设备技改后使用10年的维修费用比技改前降低多少?
参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=y-$\stackrel{∧}{b}$x.
| x(年) | 3 | 4 | 5 | 6 |
| y(万元) | 2.5 | 3 | 4 | 4.5 |
(2)已知工厂技改前该型号设备使用10年的维修费用为9万元.试根据(1)求出的线性回归方程,预测该型号设备技改后使用10年的维修费用比技改前降低多少?
参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=y-$\stackrel{∧}{b}$x.
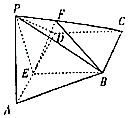 如图,四棱锥P-ABCD中,侧面PAD⊥底面ABCD,AD∥BC,AD⊥DC,AD=DC=3,BC=2,$PD=\sqrt{2}PA=\sqrt{6}$,点F在棱PG上,且FC=2FP,点E在棱AD上,且PA∥平面BEF.
如图,四棱锥P-ABCD中,侧面PAD⊥底面ABCD,AD∥BC,AD⊥DC,AD=DC=3,BC=2,$PD=\sqrt{2}PA=\sqrt{6}$,点F在棱PG上,且FC=2FP,点E在棱AD上,且PA∥平面BEF.