题目内容
已知
，
是夹角为60°的两个单位向量，则
=
+
与
=
-2
的夹角为 ．
| e1 |
| e2 |
| a |
| e1 |
| e2 |
| b |
| e1 |
| e2 |
考点：数量积表示两个向量的夹角
专题：平面向量及应用
分析：首先分别求出
=
+
与
=
-2
的数量积以及各自的模，利用数量积公式求之．
| a |
| e1 |
| e2 |
| b |
| e1 |
| e2 |
解答：
解：由已知，
•
=
，所以（
+
）（
-2
）=-
，|
+
|=
，|
-2
|=
=
+
与
=
-2
的夹角的余弦值为cos＜
+
，
-2
＞=
=
=-
，
所以
=
+
与
=
-2
的夹角为120°；
故答案为：120°．
| e1 |
| e2 |
| 1 |
| 2 |
| e1 |
| e2 |
| e1 |
| e2 |
| 3 |
| 2 |
| e1 |
| e2 |
| 3 |
| e1 |
| e2 |
| 3 |
| a |
| e1 |
| e2 |
| b |
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| e2 |
(
| ||||||||
|
|
-
| ||||
|
| 1 |
| 2 |
所以
| a |
| e1 |
| e2 |
| b |
| e1 |
| e2 |
故答案为：120°．
点评：本题考查了利用向量的数量积求向量是夹角；关键是熟练数量积公式，正确求模．
练习册系列答案
相关题目
如图，正方体ABCD-A1B1C1D1中，E、F分别为棱AB、CC1的中点，画出平面D1EF与平面ADD1A1的交线．曲线y=xex+2x+1在点（0，1）处的切线方程为（ ）
| A、x+3y-3=0 |
| B、3x-y+1=0 |
| C、3x+y-1=0 |
| D、x-3y+3=0 |
已知函数f（x）=Asin（ωx+φ），（A＞0，ω＞0，0＜φ＜π）的图象如图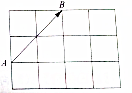
如图所示是4×3的矩形（每个小方格都是单位正方形），在起点和中点都在小方格的顶点处的向量中，试问：