题目内容

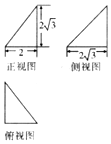
12．如图，在正方形网格纸上，粗实线画出的是某多面体的三视图及其部分尺寸，若该多面体的顶点在同一球面上，则该球的表面积等于（　　）
A．8πB．18πC．24πD．8$\sqrt{6}$π

分析 由题意，得到几何体为两个相同的四棱锥的组合体，
利用图中数据求出外接球的半径，计算表面积即可．

解答 解：由已知得几何体为两个相同的四棱锥的组合体，
其四棱锥的底面是正方形，斜高长度为3，
且外接球的球心为四棱锥的底面中心，半径为四棱锥的高，
设外接球的半径为r，四棱锥的底面边长为a，
则2a2=（2r）2…①，
r2+${（\frac{a}{2}）}^{2}$=32…②；
由①②组成方程组，解得r2=6，
所以其外接球的表面积为4πr2=24π．
故选：C．

点评 本题考查了空间几何体三视图的应用问题，解题的关键是还原出几何体的结构特征，是基础题．

练习册系列答案
相关题目
2．已知二次函数y=a（a+1）x2-（2a+1）x+1，当a=1，2，3，…，n，…时，其抛物线在x轴上截得线段长依次为d1，d2，…，dn，…，则$\underset{lim}{n→∞}$（d1+d2+…+dn）=（　　）
A．1B．2C．3D．4
3．已知M，F为椭圆的$C：\frac{x^2}{20}+\frac{y^2}{16}=1$的上顶点和右焦点，直线l与椭圆C交与A，B两点，且三角形△MAB的重心恰为F，则直线l的方程为6x-5y-28=0．
20．已知曲线E：$\frac{x^2}{a^2}+{y^2}$=1（a＞b，a≠1）上两点A（x1，y1），B（x2，y2）（x1≠x2）．
（1）若点A，B均在直线y=2x+1上，且线段AB中点的横坐标为-$\frac{1}{3}$，求a的值；
（2）记$\overrightarrow m=（\frac{x_1}{a}，{y_1}），\overrightarrow n=（\frac{x_2}{a}，{y_2}）$，若$\overrightarrow m⊥\overrightarrow n$为坐标原点，试探求△OAB的面积是否为定值？若是，求出定值；若不是，请说明理由．
7．已知某几何体的三视图如图所示，则该几何体的内切球的表面积为（　　）
A．$\frac{2π}{3}$B．$\frac{4π}{3}$C．3πD．4π
17．已知函数f（x）=lnx-mx+m（m∈R）．
（1）当m＞0时，求f′（x）+mx的最小值；
（2）若f（x）＞0在x∈（0，+∞）上有解，求实数m的取值集合M．
4．设等差数列{an}的公差d≠0，且a2=-d，若ak是a6与ak+6的等比中项，则k=（　　）
A．5B．6C．9D．11
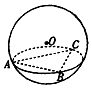1．如图，已知正三角形ABC的三个顶点都在球O的球面上，球心O到平面ABC的距离为1，且AB=3，则球O的表面积为16π．
2．在直角坐标系中，以原点为极点，x轴的正半轴为极轴建立极坐标系，直线l的极坐标方程为ρcos（θ+$\frac{π}{4}$）=$\frac{\sqrt{2}}{2}$，曲线C的参数方程为$\left\{\begin{array}{l}{x=5+cosθ}\\{y=sinθ}\end{array}\right.$（θ为参数）．
（1）求直线l的直角坐标方程和曲线C的普通方程；
（2）曲线C交x轴于A、B两点，且点A的横坐标小于点B的横坐标，P为直线l上的动点，求△PAB周长的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网