题目内容
1．
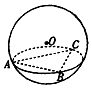如图，已知正三角形ABC的三个顶点都在球O的球面上，球心O到平面ABC的距离为1，且AB=3，则球O的表面积为16π．
分析 利用勾股定理求出球O的半径，即可求出球O的表面积．
解答 .解：设正△ABC的外接圆圆心为O1，知O1A=$\sqrt{3}$，
在Rt△OO1A中，∵球心O到平面ABC的距离为1，
∴OA=$\sqrt{3+1}$=2，
∴球O的表面积为4π×22=16π．
故答案为：16π．
点评 本题考查了球O的表面积的计算问题，解题的关键是根据条件求出球的半径，是基础题目．
练习册系列答案
相关题目
11．已知$\frac{1+2i}{a+bi}$=2-i（i为虚数单位，a，b∈R），在|a-bi|=（ ）
| A． | -i | B． | 1 | C． | 2 | D． | $\sqrt{5}$ |
12．
如图，在正方形网格纸上，粗实线画出的是某多面体的三视图及其部分尺寸，若该多面体的顶点在同一球面上，则该球的表面积等于（ ）
如图，在正方形网格纸上，粗实线画出的是某多面体的三视图及其部分尺寸，若该多面体的顶点在同一球面上，则该球的表面积等于（ ）| A． | 8π | B． | 18π | C． | 24π | D． | 8$\sqrt{6}$π |
9．已知约束条件$\left\{\begin{array}{l}{x-3y+4≥0}\\{x+2y-1≥0}\\{3x+y-8≤0}\end{array}\right.$，若目标函数z=x+ay（a≥0）在且只在点（2，2）处取得最大值，则a的取值范围为（ ）
| A． | 0＜a＜$\frac{1}{3}$ | B． | a≥$\frac{1}{3}$ | C． | a＞$\frac{1}{3}$ | D． | 0＜a＜$\frac{1}{2}$ |
16．已知定义在R上的可导函数f（x）的导函数为f'（x），满足f'（x）＜f（x），且f（0）=2，则不等式f（x）-2ex＜0的解集为（ ）
| A． | （-2，+∞） | B． | （0，+∞） | C． | （1，+∞） | D． | （4，+∞） |
6．已知某几何体的三视图如图，则该几何体的体积是（ ）
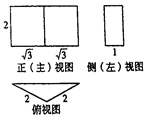
| A． | $\frac{{4\sqrt{3}}}{3}$ | B． | $4\sqrt{3}$ | C． | $2\sqrt{3}$ | D． | $\frac{{2\sqrt{3}}}{3}$ |
13．命题“?x∈R，使得x2＜1”的否定是（ ）
| A． | ?x∈R，都有x2＜1 | B． | ?x∈R，使得x2≥1 | ||
| C． | ?x∈R，都有x≤-1或x≥1 | D． | ?x∈R，使得x2＞1 |
10．质地均匀的正四面体表面分别印有0，1，2，3四个数字，某同学随机的抛掷次正四面体2次，若正四面体与地面重合的表面数字分别记为m，n，且两次结果相互独立，互不影响．记m2+n2≤4为事件A，则事件A发生的概率为（ ）
| A． | $\frac{3}{8}$ | B． | $\frac{3}{16}$ | C． | $\frac{π}{8}$ | D． | $\frac{π}{16}$ |