题目内容
19.设F1、F2是双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的两个焦点,P是C1上一点,若|PF1|+|PF2|=6a,且△PF1F2最小内角的大小为30°,抛物线C2:y2=12x的准线交双曲线C1所得的弦长为4$\sqrt{3}$,则双曲线C1的实轴长为( )| A. | 6 | B. | 2$\sqrt{6}$ | C. | $\sqrt{3}$ | D. | $2\sqrt{3}$ |
分析 设|PF1|>|PF2|,由已知条件求出|PF1|=4a,|PF2|=2a,e=$\sqrt{3}$,b=$\sqrt{2}$a,利用抛物线C2:y2=12x的准线交双曲线C1所得的弦长为4$\sqrt{3}$,可得$\frac{9}{{a}^{2}}-\frac{12}{{b}^{2}}$=1,由此能求出双曲线C1的实轴长.
解答 解:设|PF1|>|PF2|,则|PF1|-|PF2|=2a,
又|PF1|+|PF2|=6a,解得|PF1|=4a,|PF2|=2a.
则∠PF1F2是△PF1F2的最小内角为30°,
∴|PF2|2=|PF1|2+|F1F2|2-2|PF1|•|F1F2|cos30°,
∴(2a)2=(4a)2+(2c)2-2×4a×2c×$\frac{\sqrt{3}}{2}$,
同时除以a2,化简e2-2$\sqrt{3}$e+3=0,
解得e=$\sqrt{3}$,∴b=$\sqrt{2}$a①
∵抛物线C2:y2=12x的准线交双曲线C1所得的弦长为4$\sqrt{3}$,
∴$\frac{9}{{a}^{2}}-\frac{12}{{b}^{2}}$=1②,
由①②可得2a=2$\sqrt{3}$,
故选D.
点评 本题考查双曲线的定义、方程和性质,考查双曲线C1的实轴长的求法,考查三角形的余弦定理和运用,考查运算能力,属于中档题.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
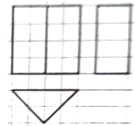 如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的外接球的表面积为32π.
如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的外接球的表面积为32π.