题目内容
6.设函数f(x)=x2-alnx-(a-2)x(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若函数f(x)有两个零点x1,x2,求满足条件的最小正整数a的值.
分析 (Ⅰ)利用导数的运算法则即可得出f′(x),并对a分类讨论即可;
(Ⅱ)由(Ⅰ)的结论,结合根的存在性原理,可以判断存在a0∈(2,3),h(a0)=0,当a>a0,h(a)>0;
解答 解:(Ⅰ)$f'(x)=2x-(a-2)-\frac{a}{x}=\frac{{2{x^2}-(a-2)x-a}}{x}=\frac{(2x-a)(x+1)}{x}$.
当a≤0时,f′(x)>0在(0,+∞)上恒成立,
所以函数f(x)单调递增区间为(0,+∞),此时f(x)无单调减区间.
当a>0时,由f′(x)>0,得$x>\frac{a}{2}$,
由f′(x)<0,得0<x<$\frac{a}{2}$,得$0<x<\frac{a}{2}$,
所以函数的单调增区间为($\frac{a}{2}$,+∞),单调减区间为(0,$\frac{a}{2}$).
(Ⅱ)由(Ⅰ)可知函数f(x)有两个零点,
所以a>0,f(x)的最小值$f(\frac{a}{2})<0$,即-a2+4a-4aln$\frac{a}{2}$<0.
因为a>0,所以$a-4+4ln\frac{a}{2}>0$.
令h(a)=a-4+4ln$\frac{a}{2}$,显然h(a)在(0,+∞)上为增函数,且h(2)=-2<0,h(3)=4ln$\frac{3}{2}$-1>0,
所以存在a0∈(2,3),h(a0)=0.
当a>a0时,h(a)>0;当0<a<a0时,h(a)<0,
所以满足条件的最小正整数a=3.
又当a=3时,F(3)=3(2-ln3)>0,F(1)=0,
所以a=3时,f(x)有两个零点.
综上所述,满足条件的最小正整数a的值为3.
点评 本题考查了利用导数求函数的单调区间以及根的存在性原理的运用.

练习册系列答案
相关题目
16.双曲线W:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)一个焦点为F(2,0),若点F到W的渐近线的距离是1,则W的离心率为( )
| A. | $\frac{4}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | 2 | D. | $\frac{1}{2}$ |
15.已知F1,F2是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的两个焦点,M(x0,y0)(x0>0,y0>0)是双曲线的渐近线上一点,满足MF1⊥MF2,如果以F2为焦点的抛物线y2=2px(p>0)经过点M,则此双曲线的离心率为( )
| A. | $2+\sqrt{3}$ | B. | $2-\sqrt{3}$ | C. | $2+\sqrt{5}$ | D. | $\sqrt{5}-2$ |
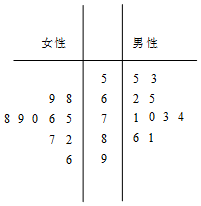 某城市为了满足市民出行的需要和节能环保的要求,在公共场所提供单车共享服务,某部门为了对该城市共享单车进行监管,随机选取了20位市民对共享单车的情况进行问卷调查,并根据其满意度评分值(满分100分)制作的茎叶图如图所示:
某城市为了满足市民出行的需要和节能环保的要求,在公共场所提供单车共享服务,某部门为了对该城市共享单车进行监管,随机选取了20位市民对共享单车的情况进行问卷调查,并根据其满意度评分值(满分100分)制作的茎叶图如图所示:
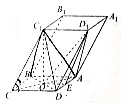 如图所示,已知底面ABCD是正方形的四棱柱ABCD-A1B1C1D1,C1C=C1D,且∠C1CB=C1CD,线段AC与BD的交点为O.
如图所示,已知底面ABCD是正方形的四棱柱ABCD-A1B1C1D1,C1C=C1D,且∠C1CB=C1CD,线段AC与BD的交点为O.