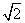��Ŀ����
��ƽ��ֱ������ϵxOy�У�����һ��ƽ��㼯��������ڷ���ƽ������a�����������P���������е�Q������ʹ��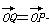 ��a�����aΪƽ��㼯����һ���������ڣ����������ĸ����⣺
��a�����aΪƽ��㼯����һ���������ڣ����������ĸ����⣺
����ƽ��㼯��������������a����ka(k��Z��k��0)Ҳ�������������ڣ�
����ƽ��㼯���γɵ�ƽ��ͼ�ε������һ�����㳣���������������������ڣ�
����ƽ��㼯����{(x��y)|x��0��y��0}����b��(��1,2)Ϊ����һ���������ڣ�
����ƽ��㼯����{(x��y)|y��|sin x|��|cos x|}����c��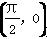 Ϊ����һ���������ڣ�
Ϊ����һ���������ڣ�
����������ĸ�����(����)
A��1 B��2 C��3 D��4
A
[����]�����ڢ٣�ȡ����{(x��y)|x��0��y��0}��a��(1,0)����aΪ�����������ڣ�����a��(��1,0)���������������ڣ��ʢ��Ǽ����⣻��֪���������⣻���ڢۣ�ȡ ����
���� ����Q∉������b��������һ���������ڣ��ʢ��Ǽ����⣻���ڢܣ�ȡ
����Q∉������b��������һ���������ڣ��ʢ��Ǽ����⣻���ڢܣ�ȡ ��(�У�1)����Q(�У�1)����|sin ��|��|cos ��|����1��1����Q∉������c��������һ���������ڣ��ʢ��Ǽ����⣮��ѡA.
��(�У�1)����Q(�У�1)����|sin ��|��|cos ��|����1��1����Q∉������c��������һ���������ڣ��ʢ��Ǽ����⣮��ѡA.

��ϰ��ϵ�д�
�����Ŀ
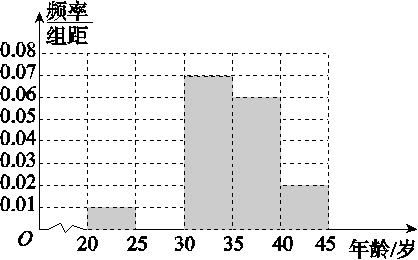
 �У���֪
�У���֪ ������n��ֵ
������n��ֵ 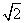 ��AB��AD����AE��ƽ��ABD��ƽ��CBD��ƽ��ABD.
��AB��AD����AE��ƽ��ABD��ƽ��CBD��ƽ��ABD.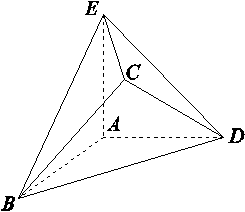
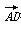 ��(2,8)��
��(2,8)��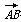 ��(��3,4)���Խ���AC��BD�ཻ�ڵ�M����
��(��3,4)���Խ���AC��BD�ཻ�ڵ�M����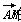 ������Ϊ(����)
������Ϊ(����)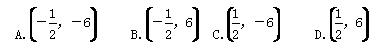

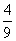 B.
B.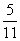 C.
C.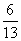 D.
D.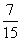
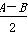 ��5cos2
��5cos2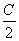 ��4����tan C�����ֵΪ(����)
��4����tan C�����ֵΪ(����)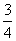 B����
B����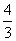 C����
C����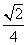 D����2
D����2