题目内容
已知函数f（x）=|x2-4x-5|，若在区间（-1，5）上，y=kx+3k的图象位于函数f（x）的上方，求k的取值范围．
考点：函数的图象
专题：数形结合,函数的性质及应用
分析：画出函数的图象，联立直线与函数组成方程组，求出k的值，利用数形结合解得k的范围．
解答：
解：当x∈（-1，5）时，f（x）=-x2+4x+5．
由y=
得x2+（k-4）x+（3k-5）=0．
令△=（k-4）2-4（3k-5）=0，解得 k=2或k=18，
在区间（-1，5）上，当k=2时，y=2（x+3）的图象与函数f（x）的图象只交于一点（1，8）；
当k=18时，y=18（x+3）的图象与函数f（x）的图象没有交点．
如图可知，由于直线y=k（x+3）过点（-3，0），
当k＞2时，直线y=k（x+3）是由直线y=2（x+3）绕点（-3，0）逆时针方向旋转得到．
因此，在区间（-1，5）上，y=k（x+3）的图象位于函数f（x）图象的上方．
故k的取值范围为：（2，+∞）．
解：当x∈（-1，5）时，f（x）=-x2+4x+5．由y=
|
令△=（k-4）2-4（3k-5）=0，解得 k=2或k=18，
在区间（-1，5）上，当k=2时，y=2（x+3）的图象与函数f（x）的图象只交于一点（1，8）；
当k=18时，y=18（x+3）的图象与函数f（x）的图象没有交点．
如图可知，由于直线y=k（x+3）过点（-3，0），
当k＞2时，直线y=k（x+3）是由直线y=2（x+3）绕点（-3，0）逆时针方向旋转得到．
因此，在区间（-1，5）上，y=k（x+3）的图象位于函数f（x）图象的上方．
故k的取值范围为：（2，+∞）．
点评：本题考查了函数图象的画法以及二次函数在定区间上的最大最小值问题，是中档题．
练习册系列答案
唐印文化课时测评系列答案
导学与测试系列答案
相关题目
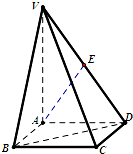如图，在四棱锥V-ABCD中，VA⊥底面ABCD，底面ABCD是边长为2的正方形．