Question

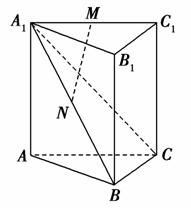
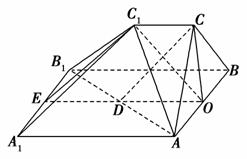
如图，多面体ABC－A₁B₁C₁中，三角形ABC是边长为4的正三角形，AA₁∥BB₁∥CC₁，AA₁⊥平面ABC，AA₁＝BB₁＝2CC₁＝4.

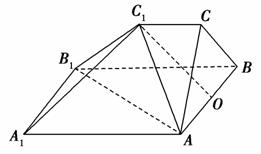
(1)若O是AB的中点，求证：OC₁⊥A₁B₁；

(2)在线段AB₁上是否存在一点D，使得CD∥平面A₁B₁C₁？若存在，确定点D的位置；若不存在，请说明理由．

Answer 1

[解析]　(1)取线段A₁B₁的中点E，连接OE，C₁E，CO，

已知等边三角形ABC的边长为4，AA₁＝BB₁＝2CC₁＝4，AA₁⊥平面ABC，AA₁∥BB₁∥CC₁，

∴四边形AA₁B₁B是正方形，OE⊥AB，CO⊥AB.

∵CO∩OE＝O，

∴AB⊥平面EOCC₁，

又A₁B₁∥AB，OC₁⊂平面EOCC₁，∴OC₁⊥A₁B₁.

(2)设OE∩AB₁＝D，连接CD，则点D是AB₁的中点，

∴ED∥AA₁，ED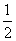＝AA₁，

又∵CC₁∥AA₁，CC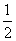₁＝AA₁，

∴四边形CC₁ED是平行四边形，

∴CD∥C₁E，∴CD∥平面A₁B₁C₁，

即存在点D，使得CD∥平面A₁B₁C₁，且点D是AB₁的中点．