题目内容
已知全集U={x|-3≤x≤8},集合A={x|-1≤x<3},B={x|2<x≤5},求:
(1)A∩B;
(2)A∪(∁UB);
(3)(∁UA)∩B.
(1)A∩B;
(2)A∪(∁UB);
(3)(∁UA)∩B.
考点:交、并、补集的混合运算
专题:集合
分析:由已知中全集U={x|-3≤x≤8},集合A={x|-1≤x<3},B={x|2<x≤5},结合集合交集,并集和补集的定义,可得答案.
解答:
解:∵全集U={x|-3≤x≤8},集合A={x|-1≤x<3},B={x|2<x≤5},
(1)A∩B2<x<3},
(2)∁UB={x|-3≤x≤2,或5<x≤8},
∴A∪(∁UB)={x|-1≤x≤2},
(3)∁UA={x|-3≤x<-1,或3≤x≤8},
∴(∁UA)∩B={x|2≤x≤5};
(1)A∩B2<x<3},
(2)∁UB={x|-3≤x≤2,或5<x≤8},
∴A∪(∁UB)={x|-1≤x≤2},
(3)∁UA={x|-3≤x<-1,或3≤x≤8},
∴(∁UA)∩B={x|2≤x≤5};
点评:本题考查的知识点是集合的交,并,补集混合运算,难度不大,属于基础题.

练习册系列答案
相关题目
(文)若a∈R,则“a2>a”是“a>1”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
若定义在R上的函数f(x)满足:对任意x1,x2∈R有f(x1+x2)=f(x1)+f(x2)+1,则下列说法一定正确的是( )
| A、f(x)-1是奇函数 |
| B、f(x)-1是偶函数 |
| C、f(x)+1是奇函数 |
| D、f(x)+1是偶函数 |
方程x2+y2+2ax+2by+a2+b2=0表示的图形是( )
| A、以(a,b)为圆心的圆 |
| B、以(-a,-b)为圆心的圆 |
| C、点(a,b) |
| D、点(-a,-b) |
如图所示,网格纸上小正方形的边长为1cm,粗实线为某空间几何体的三视图,则该几何体的体积为( )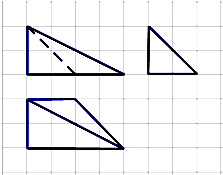

| A、2cm3 |
| B、4cm3 |
| C、6cm3 |
| D、8cm3 |