题目内容
2.方程sin(2x+$\frac{π}{3}$)+m=0在(0,π)内有相异两解α,β,则tan(α+β)=( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
分析 把方程的相异解α、β分别代入方程,得到的两个方程相减,利用和差化积公式化简,结合sin(α-β)≠0,求得cos(α+β+$\frac{π}{3}$)=0,结合范围可求α+β=$\frac{π}{6}$或$\frac{7π}{6}$,从而可求tan(α+β)的值.
解答 解:∵α、β是方程的相异解,
∴sin(2α+$\frac{π}{3}$)+m=0①.
sin(2β+$\frac{π}{3}$)+m=0②.
∴①-②得sin(2α+$\frac{π}{3}$)-sin(2β+$\frac{π}{3}$)=2cos(α+β+$\frac{π}{3}$)sin(α-β)=0,
∵α,β∈(0,π),α,β相异,可得:α-β∈(-π,π),可得:sin(α-β)≠0,
∴cos(α+β+$\frac{π}{3}$)=0,
∵α+β+$\frac{π}{3}$∈($\frac{π}{3}$,$\frac{7π}{3}$),
∴解得:α+β+$\frac{π}{3}$=$\frac{π}{2}$或$\frac{3π}{2}$,可得α+β=$\frac{π}{6}$或$\frac{7π}{6}$,
∴tan(α+β)=$\frac{\sqrt{3}}{3}$.
故选:C.
点评 本题主要考查和差化积公式,正弦函数,余弦函数的图象和性质,考查了数形结合思想的应用,解题的关键既要熟练掌握公式,又要灵活利用特殊角,属于中档题.

练习册系列答案
相关题目
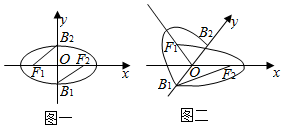
14.如图,椭圆$\frac{{x}^{2}}{3}$+y2=1的左、右焦点分别为F1,F2,短轴端点分别为B1,B2,现沿B1B2将椭圆折成120°角(图二),则异面直线F1B2与B1F2所成角的余弦值为( )

| A. | 0 | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | -$\frac{1}{3}$ |
11.已知$tan(x+\frac{π}{4})=2$,则sin2x=( )
| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{9}{10}$ |
12.函数f(x)=log3(x-1)的定义域是( )
| A. | (1,+∞) | B. | [1,+∞) | C. | {x∈R|x≠1} | D. | R |