题目内容
17.已知函数f(x)=|x-1|-2|x+1|.(I)求不等式f(x)≤-1的解集;
(Ⅱ)若关于x的不等式f(x)≥3a-1有解,求实数a的取值范围.
分析 (Ⅰ)法一:通过讨论x的范围,解出各个范围内的x的范围,求出不等式的解集即可,法二:根据函数图象求出不等式的解集即可;
(Ⅱ)法一:通过讨论x的范围,解出各个范围内的x的范围,求出不等式的最大值,问题转化为:2≥3a-1有解,法二:根据函数图象求出不等式的解集即可.
解答 解:(Ⅰ)法一:x<-1时,不等式化为x+3≤-1,解得:x≤-4,
-1≤x≤1时,不等式化为-3x-1≤-1,即x≥0,∴0≤x≤1,
x>1时,不等式化为-x-3≤-1,即x≥-2,∴x>1,
∴不等式的解集是{x|x≤-4或x≥0};
法二:f(x)=|x-1|-2|x+1|=$\left\{\begin{array}{l}{x+3,x<-1}\\{-3x-1,-1≤x≤1}\\{-x-3,x>1}\end{array}\right.$,
如图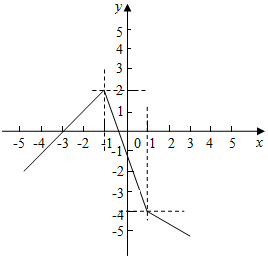
由x+3=-1,得x=-4,
由-3x-1=-1,得x=0,
∴不等式的解集是{x|x≤-4或x≥0};
(Ⅱ)法一:x<-1时,f(x)=x+3∈(-∞,2),
-1≤x≤1时,f(x)=-3x-1∈[-4,2],
x>1时,f(x)=-x-3∈(-∞,-4),
∴x=-1时,f(x)max=2,
要使关于x的不等式f(x)≥3a-1有解,
只需2≥3a-1有解,解得:a≤1,
故a的范围是(-∞,1];
法二:由f(x)的图象可知x=-1时,f(x)max=2,
要使关于x的不等式f(x)≥3a-1有解,
只需2≥3a-1有解,解得:a≤1,
故a的范围是(-∞,1].
点评 本题考查了解绝对值不等式问题,考查数形结合思想,转化思想,是一道中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.已知$\frac{m}{1+i}$=1-ni,其中,m,n是实数,i是虚数单位,则m-n=( )
| A. | 3 | B. | 2 | C. | 1 | D. | -1 |
12.若集合M={1,2,3,4},N={x|x(x-3)<0},则M∩N等于( )
| A. | {1,2,3} | B. | {1,2} | C. | {x|1<x<3} | D. | {2,3,4} |
2.方程sin(2x+$\frac{π}{3}$)+m=0在(0,π)内有相异两解α,β,则tan(α+β)=( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
7.不等式组$\left\{\begin{array}{l}{x-y-7≤0}\\{x+y-11≥0}\\{2x+y-14≥0}\\{\;}\end{array}\right.$表示的平面区域为D,若对数函数y=logax(a>0,a≠1)的图象上存在区域D上的点,则实数a的取值范围是( )
| A. | [1,3] | B. | (0,1)∪(1,3] | C. | [3,+∞) | D. | ($\frac{1}{2}$,1)∪[3,+∞) |