题目内容
已知正三棱锥P-ABC的正视图和俯视图如图所示，则此三棱柱的外接球的表面积为（ ）| A、4π | ||
| B、12π | ||
C、
| ||
D、
|
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：根据三视图判断正三棱锥的侧棱长与底面正三角形的边长，借助直观图求出外接球的半径，代入球的表面积公式计算．
解答：
解：由正视图与侧视图知，正三棱锥的侧棱长为4，底面正三角形的边长为2
，如图：
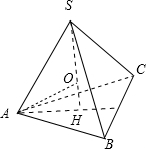
其中SA=4，AH=
×2
×
=2，SH=
=2
，
设其外接球的球心为0，半径为R，则：OS=OA=R，
∴R+
=2
⇒R=
，
∴外接球的表面积S=4π×
=
．
故选：D．
| 3 |
其中SA=4，AH=
| 2 |
| 3 |
| 3 |
| ||
| 2 |
| 16-4 |
| 3 |
设其外接球的球心为0，半径为R，则：OS=OA=R，
∴R+
| R2-4 |
| 3 |
4
| ||
| 3 |
∴外接球的表面积S=4π×
| 16 |
| 3 |
| 64π |
| 3 |
故选：D．
点评：本题考查了由三视图求几何体的外接球的表面积，根据三棱锥的结构特征求出外接球的半径是解答本题的关键．
练习册系列答案
同步拓展阅读系列答案
相关题目
抛物线C：x2=8y与直线y=2x-2相交于A，B两点，点P是抛物线C上不同A，B的一点，若直线PA，PB分别与直线y=2相交于点Q，R，O为坐标原点，则
•
的值是（ ）
| OR |
| OQ |
| A、20 | B、16 |
| C、12 | D、与点P位置有关的一个实数 |
以椭圆
+
=1（a＞b＞0）的长轴A1A2为一边向外作一等边三角形A1A2P，若随圆的一个短轴的端点B恰为三角形A1A2P的重心，则椭圆的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知F是抛物线y2=4x的焦点，准线与x轴的交点为M，点N在抛物线上，且|NF|=
|MN|，则∠FMN=（ ）
| 1 |
| 2 |
| A、30° | B、45° |
| C、60° | D、75° |
已知非零向量
，
的夹角为θ，|
+
|=
，|
-
|=1，则θ的取值范围是（ ）
| a |
| b |
| a |
| b |
| 3 |
| a |
| b |
A、0≤θ≤
| ||||
B、
| ||||
C、
| ||||
D、0＜θ＜
|
函数f（x）=lg（x+1）+lg（x-1）的奇偶性是（ ）
| A、奇函数 | B、偶函数 |
| C、非奇非偶函数 | D、既奇又偶函数 |
复数
（i为虚数单位），Z在复平面内所对应的点在（ ）
| i-1 |
| i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
为了解高中生用电脑输入汉字的水平，随机抽取了部分学生进行每分钟输入汉字个数测试，如图是根据抽样测试后的数据绘制的频率分布直方图，其中每分钟输入汉字个数的范围是[50，150]，样本数据分组为[50，70），[70，90），[90，110），[110，130），[130，150]．已知样本中每分钟输入汉字个数小于90的人数是36，则样本中每分钟输入汉字个数不小于70个且小于130个的人数是（ ）