题目内容
设命题p:ax2+2ax+1>0的解集是实数集R;命题q:0<a<1,则p是q的 .(填“充分不必要条件”“必要不充分条件”“充要条件”“既不充分也不必要条件”)
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:求出命题F的等价条件,根据充分必要条件的定义判断即可.注意a=0时命题F成立.
解答:
解:命题p:ax2+2ax+1>0的解集是实数集R?a=0或
?a=0或
?a=0或0<a<4?0≤a<4
命题q:0<a<1.
故p是q的必要不充分条件.
答案为:必要不充分条件
|
|
命题q:0<a<1.
故p是q的必要不充分条件.
答案为:必要不充分条件
点评:本题考查充分必要条件的概念,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知x,y之间的几组数据如下表:
假设根据上表数据所得线性回归方程为y=b1x+a1,某同学根据上表中前两组数据求得的直线方程为y=b2x+a2,则以下结论正确的是( )
| x | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 0 | 2 | 1 | 3 | 3 | 4 |
| A、b1>b2,a1>a2 |
| B、b1>b2,a1<a2 |
| C、b1<b2,a1>a2 |
| D、b1<b2,a1<a2 |
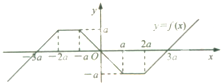 (理做)如图所示,函数y=f(x)的图象由两条射线和三条线段组成,若?x∈R,f(x)>f(x-2),则正实数的取值范围是
(理做)如图所示,函数y=f(x)的图象由两条射线和三条线段组成,若?x∈R,f(x)>f(x-2),则正实数的取值范围是