题目内容
已知{an}是等差数列,其前n项的和为Sn, {bn}是等比数列,且a1=b1=2,a4+b4=21,
S4+b4=30.
(1)求数列{an}和{bn}的通项公式;
(2)记cn=anbn,n∈N*,求数列{cn}的前n项和.
解:(1)设等差数列{an}的公差为d,等比数列{bn}的公比为q.
由a1=b1=2,得a4=2+3d,b4=2q3,S4=8+6d
由条件a4+b4=21,S4+b4=30,得方程组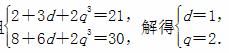
所以an=n+1,bn=2n,n∈N*.
(2)由题意知,cn=(n+1)×2n.
记Tn=c1+c2+c3+…+cn.
则Tn=c1+c2+c3+…+cn
=2×2+3×22+4×23+…+n×2n-1 +(n+1)×2n,
2 Tn= 2×22+3×23+…+(n-1)×2n-1+n×2n+ (n+1)2n+1,
所以-Tn=2×2+(22+23+…+2n )-(n+1)×2n+1,
即Tn=n·2n+1,n∈N*.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
 +2)=x+2
+2)=x+2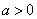 时,函数
时,函数 的图象大致是( )
的图象大致是( )
 属于特征值l的一个特征向量为α=
属于特征值l的一个特征向量为α=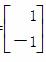 .
. 的公比大于1,
的公比大于1, ,
, ,则
,则
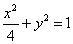 的左、右焦点.
的左、右焦点.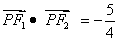 ,求点P的作标;
,求点P的作标;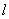 的斜率
的斜率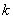 的取值范围.
的取值范围.