题目内容
17.已知函数f(x)是定义在R上的偶函数,且在(0,+∞)上单调递增,若对于任意x∈R,$f({{{log}_2}a})≤f({{x^2}-2x+2})$恒成立,则a的取值范围是( )| A. | (0,1] | B. | $[{\frac{1}{2},2}]$ | C. | (0,2] | D. | [2,+∞) |
分析 根据函数奇偶性和单调性之间的关系,将不等式进行转化即可.
解答 解:由题意f(log2a)≤f(1),
则f(|log2a|)≤f(1),
∵在区间[0,+∞)上是单调递增函数,
∴|log2a|≤1,
即-1≤log2a≤1,
解得$\frac{1}{2}$≤a≤2,
故选:B.
点评 本题主要考查不等式的求解,结合函数奇偶性和单调性之间的关系以及对数的运算性质是解决本题的关键.

练习册系列答案
相关题目
7.函数f(x)=ax+$\frac{1}{a}$(1-x),其中a>0,记f(x)在区间[0,1]上的最大值为g(a),则函数g(a)的最小值为( )
| A. | $\frac{1}{2}$ | B. | 0 | C. | 1 | D. | 2 |
5.点P在双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$(a>0,b>0)的右支上,其左、右焦点分别为F1、F2,直线PF1与以坐标原点O为圆心、a为半径的圆相切于点A,线段PF1的垂直平分线恰好过点F2,则该双曲线的渐近线的斜率为( )
| A. | ±$\frac{4}{3}$ | B. | ±$\frac{3}{4}$ | C. | ±$\frac{3}{5}$ | D. | ±$\frac{5}{3}$ |
12.已知集合M={x|x2>4},N={x|1<x<3},则N∩∁RM=( )
| A. | {x|-2≤x<4} | B. | {x|-2≤x≤2} | C. | {x|1<x≤2} | D. | {x|x<2} |
9.已知四面体ABCD的顶点都在球O表面上,且AB=BC=AC=2$\sqrt{2}$,DA=DB=DC=2,过AD作相互垂直的平面α、β,若平面α、β截球O所得截面分别为圆M、N,则( )
| A. | MN的长度是定值$\sqrt{2}$ | B. | MN长度的最小值是2 | ||
| C. | 圆M面积的最小值是2π | D. | 圆M、N的面积和是定值8π |
6.已知复数z=1+2i,则$\overline z$=( )
| A. | 1-2i | B. | 5+4i | C. | 1 | D. | 2 |
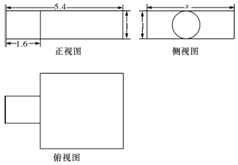 中国古代数学名著《九章算术》中记载了公元前344年商鞅制造一种标准量器----商鞅铜方升,其三视图(单位:寸)如图所示,若π取3,其体积为12.6(立方寸),则图中的x为3.
中国古代数学名著《九章算术》中记载了公元前344年商鞅制造一种标准量器----商鞅铜方升,其三视图(单位:寸)如图所示,若π取3,其体积为12.6(立方寸),则图中的x为3.