题目内容
9.已知四面体ABCD的顶点都在球O表面上,且AB=BC=AC=2$\sqrt{2}$,DA=DB=DC=2,过AD作相互垂直的平面α、β,若平面α、β截球O所得截面分别为圆M、N,则( )| A. | MN的长度是定值$\sqrt{2}$ | B. | MN长度的最小值是2 | ||
| C. | 圆M面积的最小值是2π | D. | 圆M、N的面积和是定值8π |
分析 确定DA、DB、DC两两互相垂直,M,N分别是AB,AC的中点,即可得出结论.
解答  解:∵AB=BC=AC=2$\sqrt{2}$,DA=DB=DC=2,
解:∵AB=BC=AC=2$\sqrt{2}$,DA=DB=DC=2,
∴DA、DB、DC两两互相垂直,
过AD作相互垂直的平面α、β,若平面α、β截球O所得截面分别为圆M、N,则M,N分别是AB,AC的中点,MN=$\frac{1}{2}$BC=$\sqrt{2}$,
故选A.
点评 本题考查球的内接几何体,考查学生分析解决问题的能力,确定DA、DB、DC两两互相垂直,M,N分别是AB,AC的中点是关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
17.已知函数f(x)是定义在R上的偶函数,且在(0,+∞)上单调递增,若对于任意x∈R,$f({{{log}_2}a})≤f({{x^2}-2x+2})$恒成立,则a的取值范围是( )
| A. | (0,1] | B. | $[{\frac{1}{2},2}]$ | C. | (0,2] | D. | [2,+∞) |
14.某班主任为了对本班学生的数学和物理成绩进行分析,随机抽取了8位学生的数学和物理成绩如下表.
(Ⅰ)通过对样本数据进行初步处理发现,物理成绩y与数学成绩x之间具有线性相关性,求y与x的线性回归方程(系数精确到0.01).
(Ⅱ)当某学生的数学成绩为100分时,估计该生的物理成绩.(精确到0.1分)
参考公式:回归直线的方程是:$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,其中$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y)}}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
参考数据:$\sum_{i=1}^{8}({x}_{1}-\overline{x})^{2}$=1050,$\sum_{i=1}^{8}({y}_{i}-\overline{y})^{2}$≈457,$\sum_{i=1}^{8}({x}_{1}-\overline{x})({y}_{1}-\overline{y})$≈688,$\sqrt{1050}$≈32.4.$\sqrt{457}$≈21.4,$\sqrt{550}$≈23.5.
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学分数x | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
| 物理分数y | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
(Ⅱ)当某学生的数学成绩为100分时,估计该生的物理成绩.(精确到0.1分)
参考公式:回归直线的方程是:$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,其中$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y)}}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
参考数据:$\sum_{i=1}^{8}({x}_{1}-\overline{x})^{2}$=1050,$\sum_{i=1}^{8}({y}_{i}-\overline{y})^{2}$≈457,$\sum_{i=1}^{8}({x}_{1}-\overline{x})({y}_{1}-\overline{y})$≈688,$\sqrt{1050}$≈32.4.$\sqrt{457}$≈21.4,$\sqrt{550}$≈23.5.
18.已知数列{an}满足an+1-an=2,a1=-5,则|a1|+|a2|+…+|a6|=( )
| A. | 9 | B. | 15 | C. | 18 | D. | 30 |
19.若点P为抛物线$C:{x^2}=\frac{1}{2}y$上的动点,F为抛物线C的焦点,则|PF|的最小值为( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
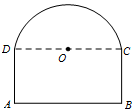 某隧道截面如图,其下部形状是矩形ABCD,上部形状是以CD为直径的半圆.已知隧道的横截面面积为4+π,设半圆的半径OC=x,隧道横截面的周长(即矩形三边长与圆弧长之和)为f(x).
某隧道截面如图,其下部形状是矩形ABCD,上部形状是以CD为直径的半圆.已知隧道的横截面面积为4+π,设半圆的半径OC=x,隧道横截面的周长(即矩形三边长与圆弧长之和)为f(x).