题目内容
7.函数f(x)=ax+$\frac{1}{a}$(1-x),其中a>0,记f(x)在区间[0,1]上的最大值为g(a),则函数g(a)的最小值为( )| A. | $\frac{1}{2}$ | B. | 0 | C. | 1 | D. | 2 |
分析 把函数变形为f(x))=(a-$\frac{1}{a}$)x+$\frac{1}{a}$,分三种情况:a>1;a=1;0<a<1进行讨论,由一次函数单调性即可求得g(a),据g(a)特征可求其最小值.
解答 解:f(x)=ax+$\frac{1}{a}$(1-x)=(a-$\frac{1}{a}$)x+$\frac{1}{a}$,
(1)当a>1时,a>$\frac{1}{a}$,f(x)是增函数,
∴f(x)在[0,1]的最大值为f(1)=a,∴g(a)=a;
(2)当a=1时,f(x)=1,∴g(a)=1;
(3)当0<a<1时,a-$\frac{1}{a}$<0,f(x)是减函数,
f(x)在[0,1]上的最大值为f(0)=$\frac{1}{a}$,∴g(a)=$\frac{1}{a}$,
所以g(a)=$\left\{\begin{array}{l}{\frac{1}{a},0<a<1}\\{1,a=1}\\{a,a>1}\end{array}\right.$,
因此g(a)最小值为1,
故选C.
点评 本题考查分段函数最值的求法,考查分类讨论思想,属中档题.

练习册系列答案
相关题目
6.已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{2}x,x>1}\\{(\frac{1}{2})^{x},x≤1}\end{array}\right.$,则f(f(-2))=( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
7.甲、乙两家外卖公司,其送餐员的日工资方案如下:甲公司的底薪70元,每单抽成4元;乙公司无底薪,40单以内(含40单)的部分每单抽成5元,超出40单的部分每单抽成7元,假设同一公司送餐员一天的送餐单数相同,现从两家公司各随机抽取一名送餐员,并分别记录其100天的送餐单数,得到如表频数表:
甲公司送餐员送餐单数频数表
乙公司送餐员送餐单数频数表
(Ⅰ)现从甲公司记录的100天中随机抽取两天,求这两天送餐单数都大于40的概率;
(Ⅱ)若将频率视为概率,回答下列问题:
(i)记乙公司送餐员日工资为X(单位:元),求X的分布列和数学期望;
(ii)小明拟到甲、乙两家公司中的一家应聘送餐员,如果仅从日工资的角度考虑,请利用所学的统计学知识为他作出选择,并说明理由.
甲公司送餐员送餐单数频数表
| 送餐单数 | 38 | 39 | 40 | 41 | 42 |
| 天数 | 20 | 40 | 20 | 10 | 10 |
| 送餐单数 | 38 | 39 | 40 | 41 | 42 |
| 天数 | 10 | 20 | 20 | 40 | 10 |
(Ⅱ)若将频率视为概率,回答下列问题:
(i)记乙公司送餐员日工资为X(单位:元),求X的分布列和数学期望;
(ii)小明拟到甲、乙两家公司中的一家应聘送餐员,如果仅从日工资的角度考虑,请利用所学的统计学知识为他作出选择,并说明理由.
4.下列说法错误的是( )
| A. | 命题,“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0“ | |
| B. | 对于命题p:?x0∈R,x02+x0+1<0,则¬p:?x∈R,x2+x+1≥0 | |
| C. | 若m,n∈R,“lnm<lnn“是“em<en”的必要不充分条件 | |
| D. | 若p∨q为假命题,则p,q均为假命题 |
17.已知函数f(x)是定义在R上的偶函数,且在(0,+∞)上单调递增,若对于任意x∈R,$f({{{log}_2}a})≤f({{x^2}-2x+2})$恒成立,则a的取值范围是( )
| A. | (0,1] | B. | $[{\frac{1}{2},2}]$ | C. | (0,2] | D. | [2,+∞) |
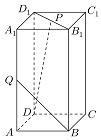 如图,设长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,Q是AA1的中点,点P在线段B1D1上;
如图,设长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,Q是AA1的中点,点P在线段B1D1上;