题目内容
解下列关于x的不等式:
(1)x2-(a+
)x+1<0(a≠0);
(2)
<0(a∈R).
(1)x2-(a+
| 1 |
| a |
(2)
| ax-1 |
| x-a |
考点:一元二次不等式的解法,其他不等式的解法
专题:不等式的解法及应用
分析:根据一元二次不等式的解法和分式不等式的解法即可得到结论.
解答:
解:(1)由x2-(a+
)x+1<0(a≠0)得(x-a)(x-
)<0(a≠0);
由a=
解得a=1或a=-1,
若a=1或a=-1时,不等式的解集为∅,
若a<-1或0<a<1时,a<
,此时不等式的解为a<x<
,
若-1<a<0或a>1时,a>
,此时不等式的解为
<x<a,
综上若a=1或a=-1时,不等式的解集为∅,
若a<-1或0<a<1时,a<
,此时不等式的解为(a,
),
若-1<a<0或a>1时,a>
,此时不等式的解为(
,a)
(2)
<0等价为(ax-1)(x-a)<0,
若a=0,不等式等价为x>0,
若a>0,不等式等价为a(x-a)(x-
)<0,即(x-a)(x-
)<0,
由(1)知若a=1时,不等式的解集为∅,
若0<a<1时,a<
,此时不等式的解为(a,
),
若a>1时,a>
,此时不等式的解为(
,a).
若a<0,不等式等价为a(x-a)(x-
)<0,即x-a)(x-
)>0,
若a=-1时,不等式的解集为{x|x≠-1},
若a<-1时,a<
,此时不等式的解集{x|x<a或x>
},
若-1<a<0时,a>
,此时不等式的解集{x|x<
或x>a}.
| 1 |
| a |
| 1 |
| a |
由a=
| 1 |
| a |
若a=1或a=-1时,不等式的解集为∅,
若a<-1或0<a<1时,a<
| 1 |
| a |
| 1 |
| a |
若-1<a<0或a>1时,a>
| 1 |
| a |
| 1 |
| a |
综上若a=1或a=-1时,不等式的解集为∅,
若a<-1或0<a<1时,a<
| 1 |
| a |
| 1 |
| a |
若-1<a<0或a>1时,a>
| 1 |
| a |
| 1 |
| a |
(2)
| ax-1 |
| x-a |
若a=0,不等式等价为x>0,
若a>0,不等式等价为a(x-a)(x-
| 1 |
| a |
| 1 |
| a |
由(1)知若a=1时,不等式的解集为∅,
若0<a<1时,a<
| 1 |
| a |
| 1 |
| a |
若a>1时,a>
| 1 |
| a |
| 1 |
| a |
若a<0,不等式等价为a(x-a)(x-
| 1 |
| a |
| 1 |
| a |
若a=-1时,不等式的解集为{x|x≠-1},
若a<-1时,a<
| 1 |
| a |
| 1 |
| a |
若-1<a<0时,a>
| 1 |
| a |
| 1 |
| a |
点评:本题主要考查不等式的求解,注意分类讨论.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
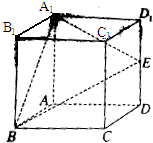 如图,正方体ABCD-A1B1C1D1中,E是棱DD1的中点,F是侧面CDD1C1上的动点,且B1F∥平面A1BE,则B1F与平面CDD1C1所成角的正弦值构成的集合是 ( )
如图,正方体ABCD-A1B1C1D1中,E是棱DD1的中点,F是侧面CDD1C1上的动点,且B1F∥平面A1BE,则B1F与平面CDD1C1所成角的正弦值构成的集合是 ( )| A、{2} | ||||||||
B、
| ||||||||
C、{t|
| ||||||||
D、{t|
|
将函数f(x)=3sin(2x+
)-1的图形按向量
=(m,n)平移后得到函数g(x)=3sin2x的图形则向量
的一个可能值是( )
| π |
| 3 |
| a |
| a |
A、(-
| ||
B、(-
| ||
C、(
| ||
D、(
|
在平面直角坐标系xOy中,设不等式组
,所表示的平面区域为D,若D的边界是菱形,则ab=( )
|
A、-2
| ||
B、2
| ||
C、2
| ||
D、-2
|
 如图,已知?ABCD中,E是AB的中点,F是BE的中点,DF,CE相较于点O,已知
如图,已知?ABCD中,E是AB的中点,F是BE的中点,DF,CE相较于点O,已知